Ordered Logistic or Probit Regression

Fits a logistic or probit regression model to an ordered factor response. The default logistic case is proportional odds logistic regression, after which the function is named.

polr(formula, data, weights, start, ..., subset, na.action,
     contrasts = NULL, Hess = FALSE, model = TRUE,
     method = c("logistic", "probit", "loglog", "cloglog", "cauchit"))

Arguments

formula

a formula expression as for regression models, of the form response ~ predictors. The response should be a factor (preferably an ordered factor), which will be interpreted as an ordinal response, with levels ordered as in the factor. The model must have an intercept: attempts to remove one will lead to a warning and be ignored. An offset may be used. See the documentation of formula for other details.
data

an optional data frame in which to interpret the variables occurring in formula.
weights

optional case weights in fitting. Default to 1.
start

initial values for the parameters. This is in the format c(coefficients, zeta): see the Values section.
...

additional arguments to be passed to optim, most often a control argument.
subset

expression saying which subset of the rows of the data should be used in the fit. All observations are included by default.
na.action

a function to filter missing data.
contrasts

a list of contrasts to be used for some or all of the factors appearing as variables in the model formula.
Hess

logical for whether the Hessian (the observed information matrix) should be returned. Use this if you intend to call summary or vcov on the fit.
model

logical for whether the model matrix should be returned.
method

logistic or probit or (complementary) log-log or cauchit (corresponding to a Cauchy latent variable).

Details

This model is what Agresti (2002) calls a cumulative link model. The basic interpretation is as a coarsened version of a latent variable \(Y_i\) which has a logistic or normal or extreme-value or Cauchy distribution with scale parameter one and a linear model for the mean. The ordered factor which is observed is which bin \(Y_i\) falls into with breakpoints $$\zeta_0 = -\infty < \zeta_1 < \cdots < \zeta_K = \infty$$ This leads to the model $$\mbox{logit} P(Y \le k | x) = \zeta_k - \eta$$ with logit replaced by probit for a normal latent variable, and \(\eta\) being the linear predictor, a linear function of the explanatory variables (with no intercept). Note that it is quite common for other software to use the opposite sign for \(\eta\) (and hence the coefficients beta).

In the logistic case, the left-hand side of the last display is the log odds of category \(k\) or less, and since these are log odds which differ only by a constant for different \(k\), the odds are proportional. Hence the term proportional odds logistic regression.

The log-log and complementary log-log links are the increasing functions \(F^{-1}(p) = -log(-log(p))\) and \(F^{-1}(p) = log(-log(1-p))\); some call the first the ‘negative log-log’ link. These correspond to a latent variable with the extreme-value distribution for the maximum and minimum respectively.

A proportional hazards model for grouped survival times can be obtained by using the complementary log-log link with grouping ordered by increasing times.

predict, summary, vcov, anova, model.frame and an extractAIC method for use with stepAIC (and step). There are also profile and confint methods.

Value

A object of class "polr". This has components

coefficients

the coefficients of the linear predictor, which has no intercept.

zeta

the intercepts for the class boundaries.

deviance

the residual deviance.

fitted.values

a matrix, with a column for each level of the response.

lev

the names of the response levels.

terms

the terms structure describing the model.

df.residual

the number of residual degrees of freedoms, calculated using the weights.

edf

the (effective) number of degrees of freedom used by the model

n, nobs

the (effective) number of observations, calculated using the weights. (nobs is for use by stepAIC.

call

the matched call.

method

the matched method used.

convergence

the convergence code returned by optim.

niter

the number of function and gradient evaluations used by optim.

lp

the linear predictor (including any offset).

Hessian

(if Hess is true). Note that this is a numerical approximation derived from the optimization proces.

model

(if model is true).

Note

The vcov method uses the approximate Hessian: for reliable results the model matrix should be sensibly scaled with all columns having range the order of one.

Prior to version 7.3-32, method = "cloglog" confusingly gave the log-log link, implicitly assuming the first response level was the ‘best’.

References

Agresti, A. (2002) Categorical Data. Second edition. Wiley.

Venables, W. N. and Ripley, B. D. (2002) Modern Applied Statistics with S. Fourth edition. Springer.

See also

optim, glm, multinom.

Examples

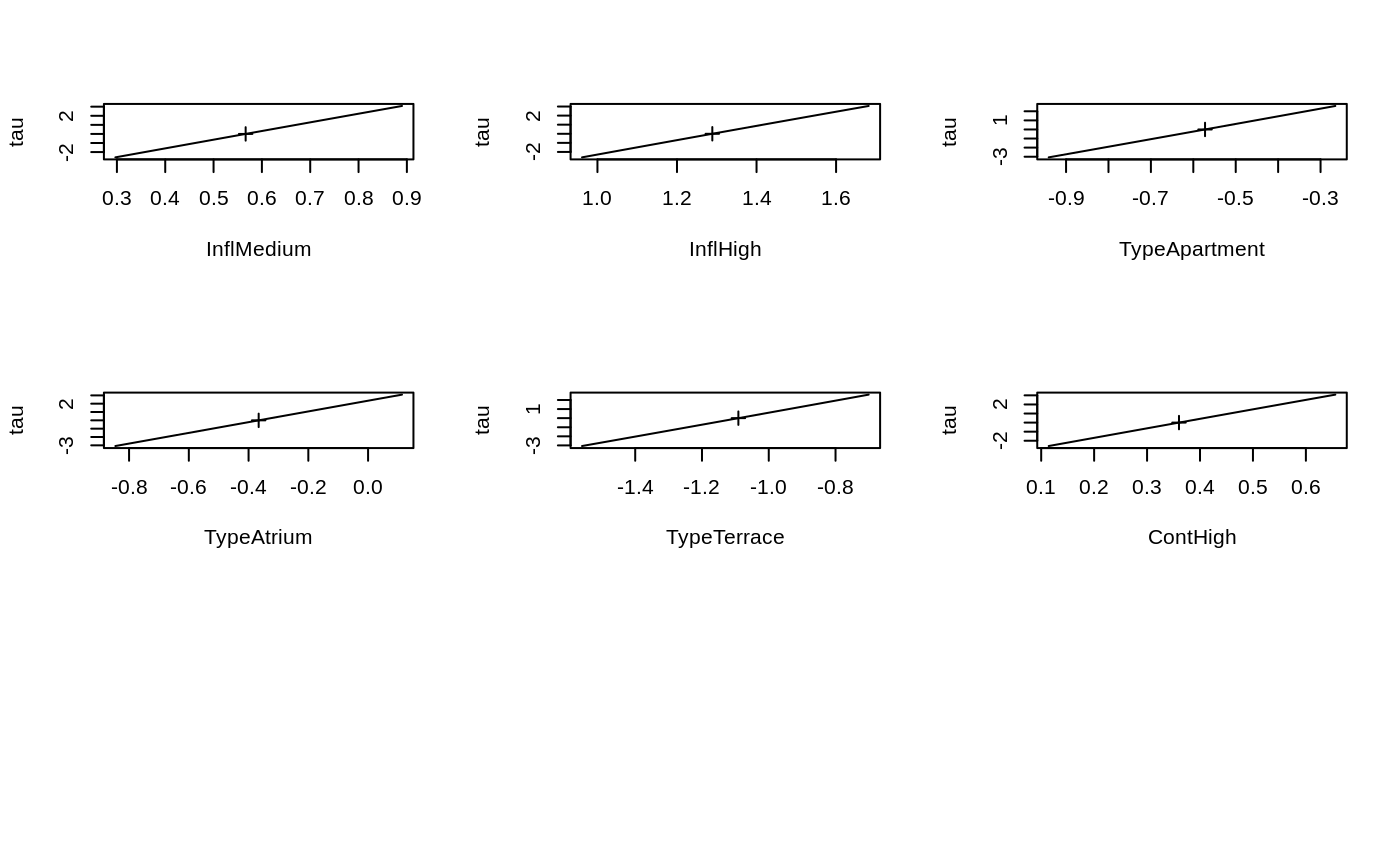
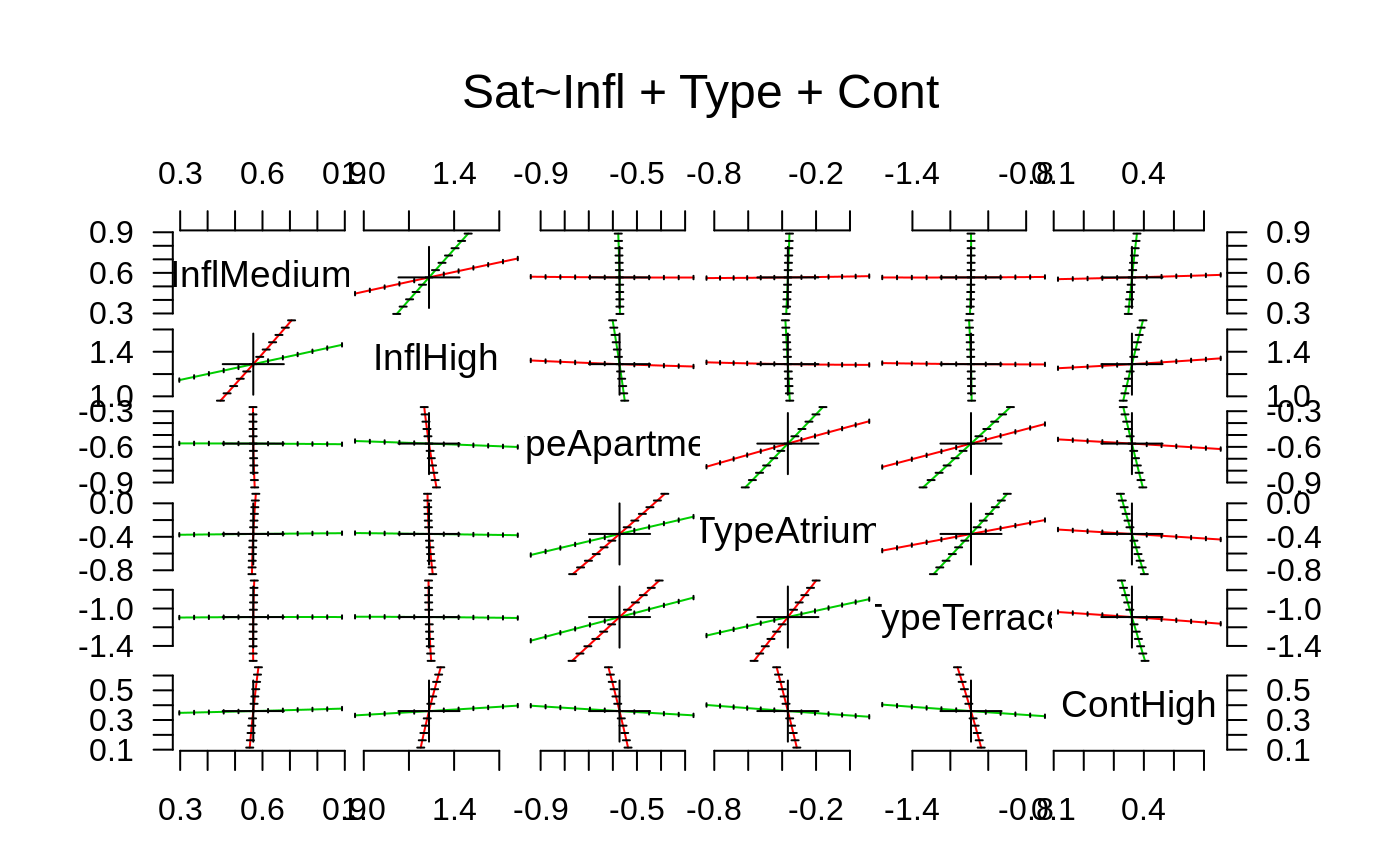
options(contrasts = c("contr.treatment", "contr.poly"))
house.plr <- polr(Sat ~ Infl + Type + Cont, weights = Freq, data = housing)
house.plr
#> Call:
#> polr(formula = Sat ~ Infl + Type + Cont, data = housing, weights = Freq)
#> 
#> Coefficients:
#>    InflMedium      InflHigh TypeApartment    TypeAtrium   TypeTerrace 
#>     0.5663937     1.2888191    -0.5723501    -0.3661866    -1.0910149 
#>      ContHigh 
#>     0.3602841 
#> 
#> Intercepts:
#>  Low|Medium Medium|High 
#>  -0.4961353   0.6907083 
#> 
#> Residual Deviance: 3479.149 
#> AIC: 3495.149 
summary(house.plr, digits = 3)
#> 
#> Re-fitting to get Hessian
#> Call:
#> polr(formula = Sat ~ Infl + Type + Cont, data = housing, weights = Freq)
#> 
#> Coefficients:
#>                Value Std. Error t value
#> InflMedium     0.566     0.1047    5.41
#> InflHigh       1.289     0.1272   10.14
#> TypeApartment -0.572     0.1192   -4.80
#> TypeAtrium    -0.366     0.1552   -2.36
#> TypeTerrace   -1.091     0.1515   -7.20
#> ContHigh       0.360     0.0955    3.77
#> 
#> Intercepts:
#>             Value  Std. Error t value
#> Low|Medium  -0.496  0.125     -3.974 
#> Medium|High  0.691  0.125      5.505 
#> 
#> Residual Deviance: 3479.149 
#> AIC: 3495.149 
## slightly worse fit from
summary(update(house.plr, method = "probit", Hess = TRUE), digits = 3)
#> Call:
#> polr(formula = Sat ~ Infl + Type + Cont, data = housing, weights = Freq, 
#>     Hess = TRUE, method = "probit")
#> 
#> Coefficients:
#>                Value Std. Error t value
#> InflMedium     0.346     0.0641    5.40
#> InflHigh       0.783     0.0764   10.24
#> TypeApartment -0.348     0.0723   -4.81
#> TypeAtrium    -0.218     0.0948   -2.30
#> TypeTerrace   -0.664     0.0918   -7.24
#> ContHigh       0.222     0.0581    3.83
#> 
#> Intercepts:
#>             Value  Std. Error t value
#> Low|Medium  -0.300  0.076     -3.937 
#> Medium|High  0.427  0.076      5.585 
#> 
#> Residual Deviance: 3479.689 
#> AIC: 3495.689 
## although it is not really appropriate, can fit
summary(update(house.plr, method = "loglog", Hess = TRUE), digits = 3)
#> Call:
#> polr(formula = Sat ~ Infl + Type + Cont, data = housing, weights = Freq, 
#>     Hess = TRUE, method = "loglog")
#> 
#> Coefficients:
#>                Value Std. Error t value
#> InflMedium     0.367     0.0727    5.05
#> InflHigh       0.790     0.0806    9.81
#> TypeApartment -0.349     0.0757   -4.61
#> TypeAtrium    -0.196     0.0988   -1.98
#> TypeTerrace   -0.698     0.1043   -6.69
#> ContHigh       0.268     0.0636    4.21
#> 
#> Intercepts:
#>             Value  Std. Error t value
#> Low|Medium   0.086  0.083      1.038 
#> Medium|High  0.892  0.087     10.223 
#> 
#> Residual Deviance: 3491.41 
#> AIC: 3507.41 
summary(update(house.plr, method = "cloglog", Hess = TRUE), digits = 3)
#> Call:
#> polr(formula = Sat ~ Infl + Type + Cont, data = housing, weights = Freq, 
#>     Hess = TRUE, method = "cloglog")
#> 
#> Coefficients:
#>                Value Std. Error t value
#> InflMedium     0.382     0.0703    5.44
#> InflHigh       0.915     0.0926    9.89
#> TypeApartment -0.407     0.0861   -4.73
#> TypeAtrium    -0.281     0.1111   -2.52
#> TypeTerrace   -0.742     0.1013   -7.33
#> ContHigh       0.209     0.0651    3.21
#> 
#> Intercepts:
#>             Value  Std. Error t value
#> Low|Medium  -0.796  0.090     -8.881 
#> Medium|High  0.055  0.086      0.647 
#> 
#> Residual Deviance: 3484.053 
#> AIC: 3500.053 

predict(house.plr, housing, type = "p")
#>          Low    Medium      High
#> 1  0.3784493 0.2876752 0.3338755
#> 2  0.3784493 0.2876752 0.3338755
#> 3  0.3784493 0.2876752 0.3338755
#> 4  0.2568264 0.2742122 0.4689613
#> 5  0.2568264 0.2742122 0.4689613
#> 6  0.2568264 0.2742122 0.4689613
#> 7  0.1436924 0.2110836 0.6452240
#> 8  0.1436924 0.2110836 0.6452240
#> 9  0.1436924 0.2110836 0.6452240
#> 10 0.5190445 0.2605077 0.2204478
#> 11 0.5190445 0.2605077 0.2204478
#> 12 0.5190445 0.2605077 0.2204478
#> 13 0.3798514 0.2875965 0.3325521
#> 14 0.3798514 0.2875965 0.3325521
#> 15 0.3798514 0.2875965 0.3325521
#> 16 0.2292406 0.2643196 0.5064398
#> 17 0.2292406 0.2643196 0.5064398
#> 18 0.2292406 0.2643196 0.5064398
#> 19 0.4675584 0.2745383 0.2579033
#> 20 0.4675584 0.2745383 0.2579033
#> 21 0.4675584 0.2745383 0.2579033
#> 22 0.3326236 0.2876008 0.3797755
#> 23 0.3326236 0.2876008 0.3797755
#> 24 0.3326236 0.2876008 0.3797755
#> 25 0.1948548 0.2474226 0.5577225
#> 26 0.1948548 0.2474226 0.5577225
#> 27 0.1948548 0.2474226 0.5577225
#> 28 0.6444840 0.2114256 0.1440905
#> 29 0.6444840 0.2114256 0.1440905
#> 30 0.6444840 0.2114256 0.1440905
#> 31 0.5071210 0.2641196 0.2287594
#> 32 0.5071210 0.2641196 0.2287594
#> 33 0.5071210 0.2641196 0.2287594
#> 34 0.3331573 0.2876330 0.3792097
#> 35 0.3331573 0.2876330 0.3792097
#> 36 0.3331573 0.2876330 0.3792097
#> 37 0.2980880 0.2837746 0.4181374
#> 38 0.2980880 0.2837746 0.4181374
#> 39 0.2980880 0.2837746 0.4181374
#> 40 0.1942209 0.2470589 0.5587202
#> 41 0.1942209 0.2470589 0.5587202
#> 42 0.1942209 0.2470589 0.5587202
#> 43 0.1047770 0.1724227 0.7228003
#> 44 0.1047770 0.1724227 0.7228003
#> 45 0.1047770 0.1724227 0.7228003
#> 46 0.4294564 0.2820629 0.2884807
#> 47 0.4294564 0.2820629 0.2884807
#> 48 0.4294564 0.2820629 0.2884807
#> 49 0.2993357 0.2839753 0.4166890
#> 50 0.2993357 0.2839753 0.4166890
#> 51 0.2993357 0.2839753 0.4166890
#> 52 0.1718050 0.2328648 0.5953302
#> 53 0.1718050 0.2328648 0.5953302
#> 54 0.1718050 0.2328648 0.5953302
#> 55 0.3798387 0.2875972 0.3325641
#> 56 0.3798387 0.2875972 0.3325641
#> 57 0.3798387 0.2875972 0.3325641
#> 58 0.2579546 0.2745537 0.4674917
#> 59 0.2579546 0.2745537 0.4674917
#> 60 0.2579546 0.2745537 0.4674917
#> 61 0.1444202 0.2117081 0.6438717
#> 62 0.1444202 0.2117081 0.6438717
#> 63 0.1444202 0.2117081 0.6438717
#> 64 0.5583813 0.2471826 0.1944361
#> 65 0.5583813 0.2471826 0.1944361
#> 66 0.5583813 0.2471826 0.1944361
#> 67 0.4178031 0.2838213 0.2983756
#> 68 0.4178031 0.2838213 0.2983756
#> 69 0.4178031 0.2838213 0.2983756
#> 70 0.2584149 0.2746916 0.4668935
#> 71 0.2584149 0.2746916 0.4668935
#> 72 0.2584149 0.2746916 0.4668935
addterm(house.plr, ~.^2, test = "Chisq")
#> Single term additions
#> 
#> Model:
#> Sat ~ Infl + Type + Cont
#>           Df    AIC     LRT   Pr(Chi)    
#> <none>       3495.1                      
#> Infl:Type  6 3484.6 22.5093 0.0009786 ***
#> Infl:Cont  2 3498.9  0.2090 0.9007957    
#> Type:Cont  3 3492.5  8.6662 0.0340752 *  
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
house.plr2 <- stepAIC(house.plr, ~.^2)
#> Start:  AIC=3495.15
#> Sat ~ Infl + Type + Cont
#> 
#>             Df    AIC
#> + Infl:Type  6 3484.6
#> + Type:Cont  3 3492.5
#> <none>         3495.1
#> + Infl:Cont  2 3498.9
#> - Cont       1 3507.5
#> - Type       3 3545.1
#> - Infl       2 3599.4
#> 
#> Step:  AIC=3484.64
#> Sat ~ Infl + Type + Cont + Infl:Type
#> 
#>             Df    AIC
#> + Type:Cont  3 3482.7
#> <none>         3484.6
#> + Infl:Cont  2 3488.5
#> - Infl:Type  6 3495.1
#> - Cont       1 3497.8
#> 
#> Step:  AIC=3482.69
#> Sat ~ Infl + Type + Cont + Infl:Type + Type:Cont
#> 
#>             Df    AIC
#> <none>         3482.7
#> - Type:Cont  3 3484.6
#> + Infl:Cont  2 3486.6
#> - Infl:Type  6 3492.5
house.plr2$anova
#> Stepwise Model Path 
#> Analysis of Deviance Table
#> 
#> Initial Model:
#> Sat ~ Infl + Type + Cont
#> 
#> Final Model:
#> Sat ~ Infl + Type + Cont + Infl:Type + Type:Cont
#> 
#> 
#>          Step Df  Deviance Resid. Df Resid. Dev      AIC
#> 1                               1673   3479.149 3495.149
#> 2 + Infl:Type  6 22.509347      1667   3456.640 3484.640
#> 3 + Type:Cont  3  7.945029      1664   3448.695 3482.695
anova(house.plr, house.plr2)
#> Likelihood ratio tests of ordinal regression models
#> 
#> Response: Sat
#>                                        Model Resid. df Resid. Dev   Test    Df
#> 1                         Infl + Type + Cont      1673   3479.149             
#> 2 Infl + Type + Cont + Infl:Type + Type:Cont      1664   3448.695 1 vs 2     9
#>   LR stat.      Pr(Chi)
#> 1                      
#> 2 30.45438 0.0003670555

house.plr <- update(house.plr, Hess=TRUE)
pr <- profile(house.plr)
confint(pr)
#>                    2.5 %      97.5 %
#> InflMedium     0.3616415  0.77195375
#> InflHigh       1.0409701  1.53958138
#> TypeApartment -0.8069590 -0.33940432
#> TypeAtrium    -0.6705862 -0.06204495
#> TypeTerrace   -1.3893863 -0.79533958
#> ContHigh       0.1733589  0.54792854
plot(pr)
pairs(pr)