Diagnostics plots for generalized linear models

Makes plot of jackknife deviance residuals against linear predictor, normal scores plots of standardized deviance residuals, plot of approximate Cook statistics against leverage/(1-leverage), and case plot of Cook statistic.

glm.diag.plots(glmfit, glmdiag = glm.diag(glmfit), subset = NULL,
               iden = FALSE, labels = NULL, ret = FALSE)

Arguments

glmfit	`glm.object` : the result of a call to `glm()`
glmdiag	Diagnostics of `glmfit` obtained from a call to `glm.diag`. If it is not supplied then it is calculated.
subset	Subset of `data` for which `glm` fitting performed: should be the same as the `subset` option used in the call to `glm()` which generated `glmfit`. Needed only if the `subset=` option was used in the call to `glm`.
iden	A logical argument. If `TRUE` then, after the plots are drawn, the user will be prompted for an integer between 0 and 4. A positive integer will select a plot and invoke `identify()` on that plot. After exiting `identify()`, the user is again prompted, this loop continuing until the user responds to the prompt with 0. If `iden` is `FALSE` (default) the user cannot interact with the plots.
labels	A vector of labels for use with `identify()` if `iden` is `TRUE`. If it is not supplied then the labels are derived from `glmfit`.
ret	A logical argument indicating if `glmdiag` should be returned. The default is `FALSE`.

Value

If ret is TRUE then the value of glmdiag is returned otherwise there is no returned value.

Details

The diagnostics required for the plots are calculated by glm.diag. These are then used to produce the four plots on the current graphics device.

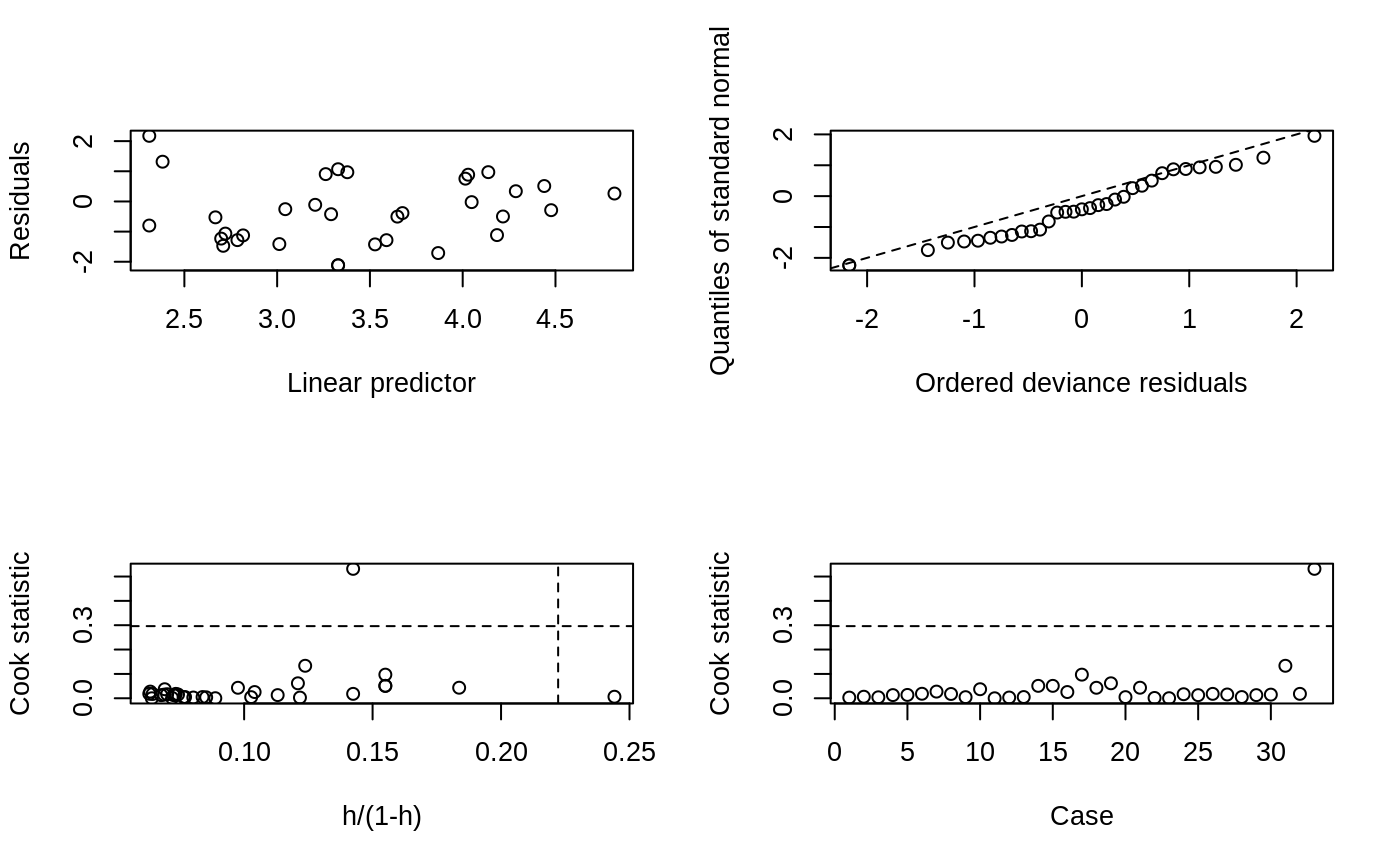
The plot on the top left is a plot of the jackknife deviance residuals against the fitted values.

The plot on the top right is a normal QQ plot of the standardized deviance residuals. The dotted line is the expected line if the standardized residuals are normally distributed, i.e. it is the line with intercept 0 and slope 1.

The bottom two panels are plots of the Cook statistics. On the left is a plot of the Cook statistics against the standardized leverages. In general there will be two dotted lines on this plot. The horizontal line is at 8/(n-2p) where n is the number of observations and p is the number of parameters estimated. Points above this line may be points with high influence on the model. The vertical line is at 2p/(n-2p) and points to the right of this line have high leverage compared to the variance of the raw residual at that point. If all points are below the horizontal line or to the left of the vertical line then the line is not shown.

The final plot again shows the Cook statistic this time plotted against case number enabling us to find which observations are influential.

Use of iden=T is encouraged for proper exploration of these four plots as a guide to how well the model fits the data and whether certain observations have an unduly large effect on parameter estimates.

Side Effects

The current device is cleared and four plots are plotted by use of split.screen(c(2,2)). If iden is TRUE, interactive identification of points is enabled. All screens are closed, but not cleared, on termination of the function.

References

Davison, A. C. and Hinkley, D. V. (1997) Bootstrap Methods and Their Application. Cambridge University Press.

Davison, A.C. and Snell, E.J. (1991) Residuals and diagnostics. In Statistical Theory and Modelling: In Honour of Sir David Cox D.V. Hinkley, N. Reid, and E.J. Snell (editors), 83--106. Chapman and Hall.

Examples

# In this example we look at the leukaemia data which was looked at in 
# Example 7.1 of Davison and Hinkley (1997)
data(leuk, package = "MASS")
leuk.mod <- glm(time ~ ag-1+log10(wbc), family = Gamma(log), data = leuk)
leuk.diag <- glm.diag(leuk.mod)
glm.diag.plots(leuk.mod, leuk.diag)