Add a Saddlepoint Approximation to a Plot

This function adds a line corresponding to a saddlepoint density or distribution function approximation to the current plot.

# S3 method for saddle.distn
lines(x, dens = TRUE, h = function(u) u, J = function(u) 1,
      npts = 50, lty = 1, ...)

Arguments

x	An object of class "saddle.distn" (see saddle.distn.object representing a saddlepoint approximation to a distribution.
dens	A logical variable indicating whether the saddlepoint density (TRUE; the default) or the saddlepoint distribution function (FALSE) should be plotted.
h	Any transformation of the variable that is required. Its first argument must be the value at which the approximation is being performed and the function must be vectorized.
J	When dens=TRUE this function specifies the Jacobian for any transformation that may be necessary. The first argument of J must the value at which the approximation is being performed and the function must be vectorized. If h is supplied J must also be supplied and both must have the same argument list.
npts	The number of points to be used for the plot. These points will be evenly spaced over the range of points used in finding the saddlepoint approximation.
lty	The line type to be used.
...	Any additional arguments to h and J.

Value

sad.d is returned invisibly.

Side Effects

A line is added to the current plot.

Details

The function uses smooth.spline to produce the saddlepoint curve. When dens=TRUE the spline is on the log scale and when dens=FALSE it is on the probit scale.

See also

saddle.distn

References

Davison, A.C. and Hinkley, D.V. (1997) Bootstrap Methods and Their Application. Cambridge University Press.

Examples

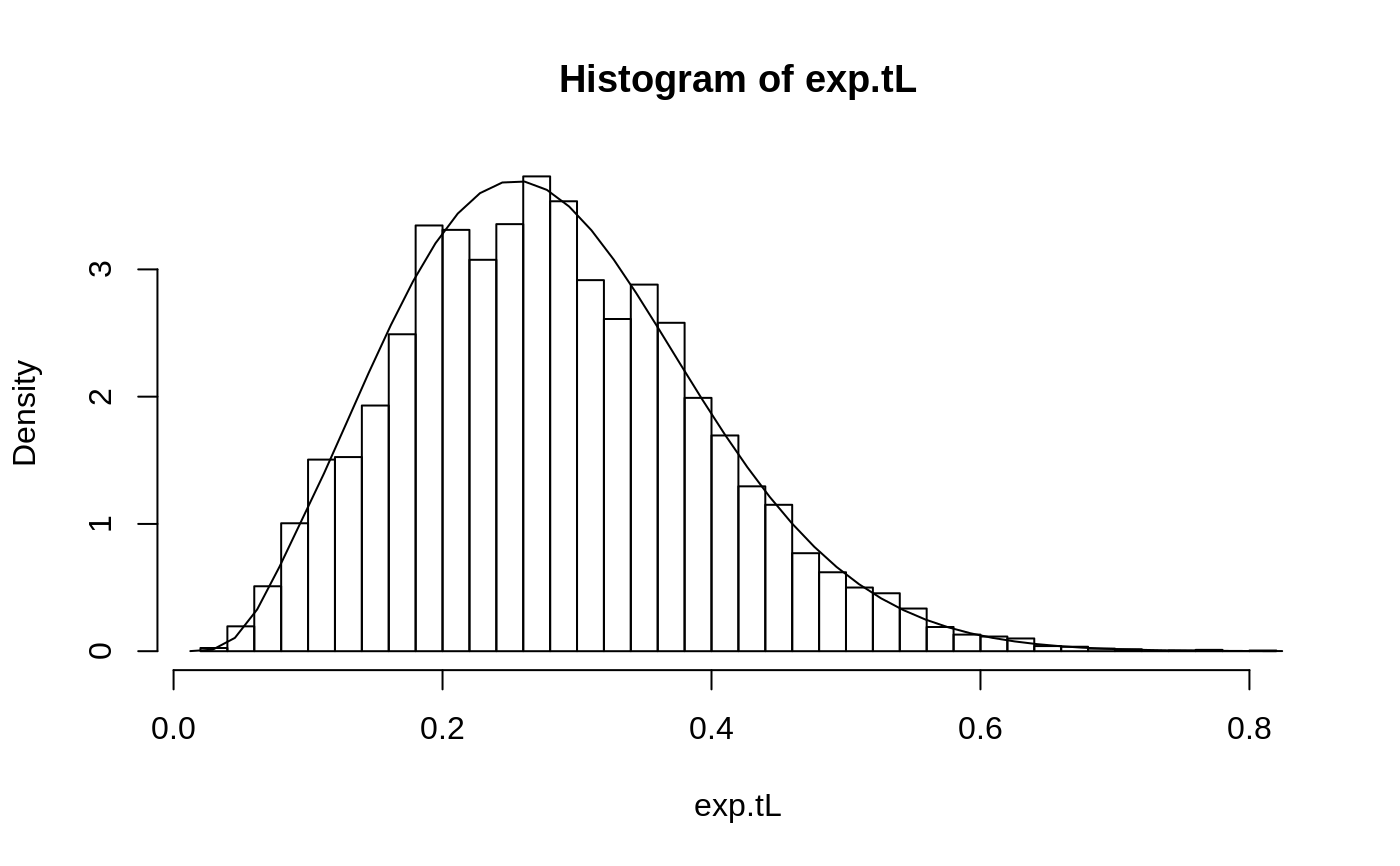
# In this example we show how a plot such as that in Figure 9.9 of
# Davison and Hinkley (1997) may be produced.  Note the large number of
# bootstrap replicates required in this example.
expdata <- rexp(12)
vfun <- function(d, i) {
     n <- length(d)
     (n-1)/n*var(d[i])
}
exp.boot <- boot(expdata,vfun, R = 9999)
exp.L <- (expdata - mean(expdata))^2 - exp.boot$t0
exp.tL <- linear.approx(exp.boot, L = exp.L)
hist(exp.tL, nclass = 50, probability = TRUE)
exp.t0 <- c(0, sqrt(var(exp.boot$t)))
exp.sp <- saddle.distn(A = exp.L/12,wdist = "m", t0 = exp.t0)

# The saddlepoint approximation in this case is to the density of
# t-t0 and so t0 must be added for the plot.
lines(exp.sp, h = function(u, t0) u+t0, J = function(u, t0) 1,
      t0 = exp.boot$t0)