Plots of the Output of a Bootstrap Simulation

This takes a bootstrap object and produces plots for the bootstrap replicates of the variable of interest.

# S3 method for boot
plot(x, index = 1, t0 = NULL, t = NULL, jack = FALSE,
     qdist = "norm", nclass = NULL, df, ...)

Arguments

x	An object of class `"boot"` returned from one of the bootstrap generation functions.
index	The index of the variable of interest within the output of `boot.out`. This is ignored if `t` and `t0` are supplied.
t0	The original value of the statistic. This defaults to `boot.out$t0[index]` unless `t` is supplied when it defaults to `NULL`. In that case no vertical line is drawn on the histogram.
t	The bootstrap replicates of the statistic. Usually this will take on its default value of `boot.out$t[,index]`, however it may be useful sometimes to supply a different set of values which are a function of `boot.out$t`.
jack	A logical value indicating whether a jackknife-after-bootstrap plot is required. The default is not to produce such a plot.
qdist	The distribution against which the Q-Q plot should be drawn. At present `"norm"` (normal distribution - the default) and `"chisq"` (chi-squared distribution) are the only possible values.
nclass	An integer giving the number of classes to be used in the bootstrap histogram. The default is the integer between 10 and 100 closest to `ceiling(length(t)/25)`.
df	If `qdist` is `"chisq"` then this is the degrees of freedom for the chi-squared distribution to be used. It is a required argument in that case.
...	When `jack` is `TRUE` additional parameters to `jack.after.boot` can be supplied. See the help file for `jack.after.boot` for details of the possible parameters.

Value

boot.out is returned invisibly.

Side Effects

All screens are closed and cleared and a number of plots are produced on the current graphics device. Screens are closed but not cleared at termination of this function.

Details

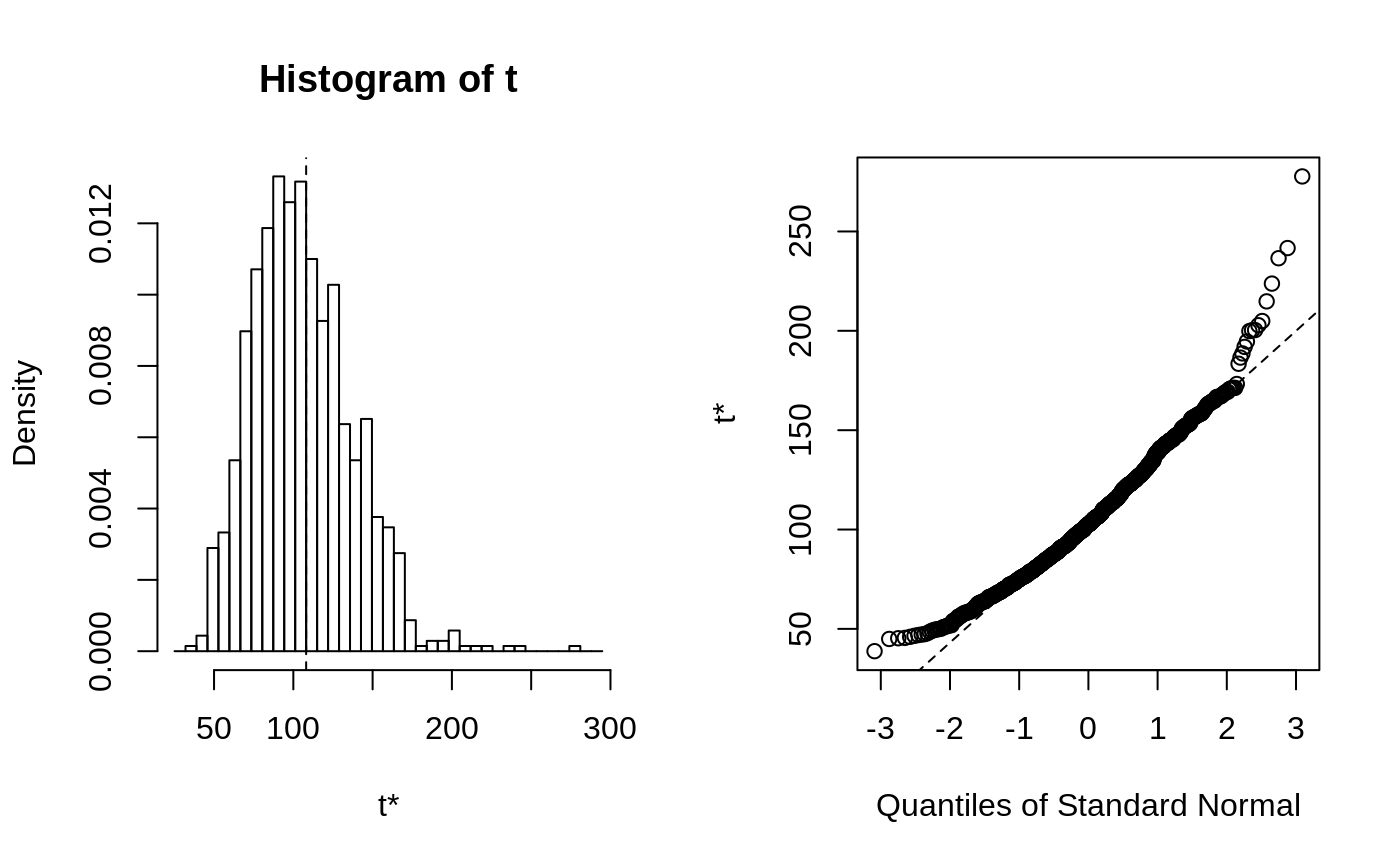
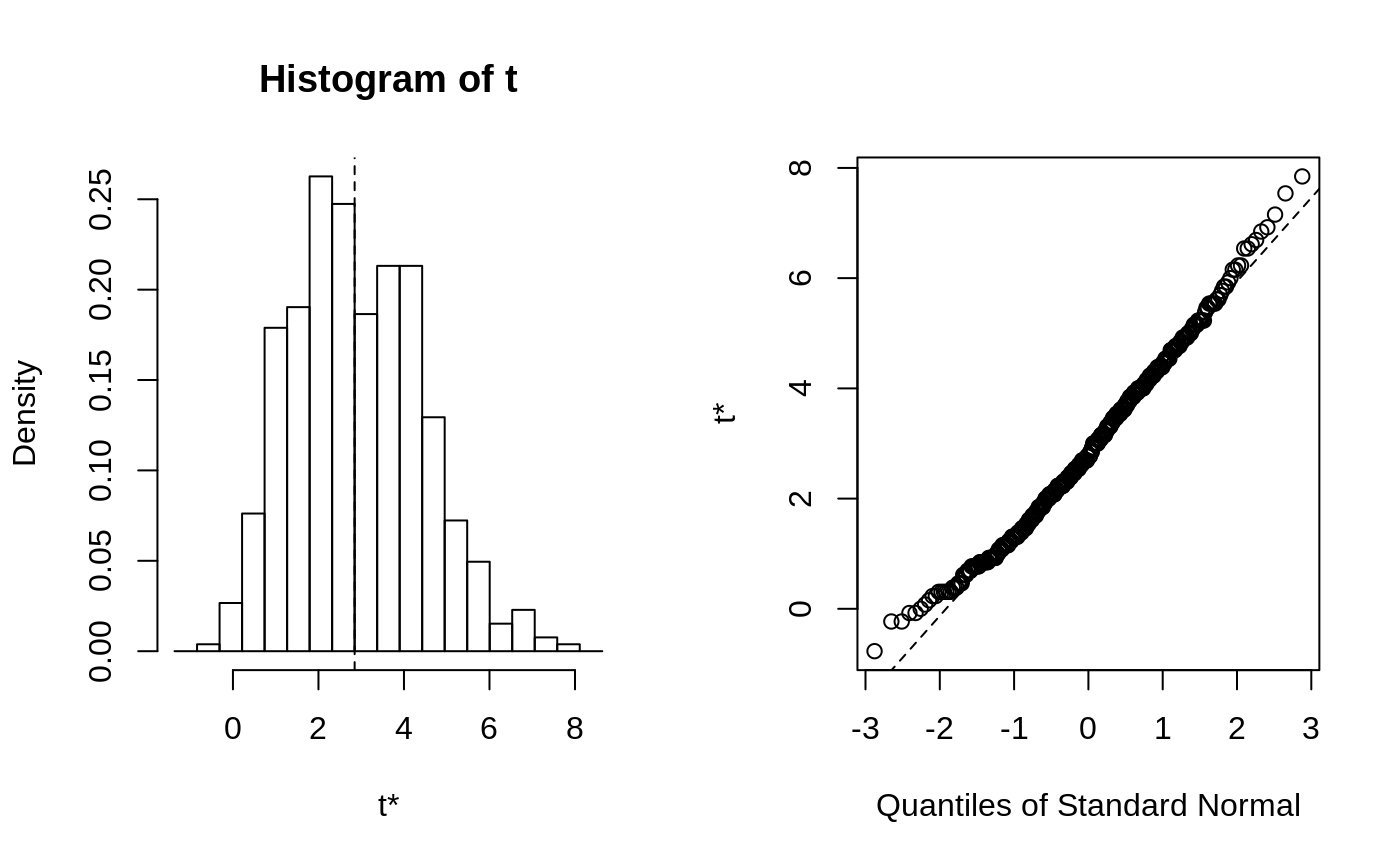
This function will generally produce two side-by-side plots. The left plot will be a histogram of the bootstrap replicates. Usually the breaks of the histogram will be chosen so that t0 is at a breakpoint and all intervals are of equal length. A vertical dotted line indicates the position of t0. This cannot be done if t is supplied but t0 is not and so, in that case, the breakpoints are computed by hist using the nclass argument and no vertical line is drawn.

The second plot is a Q-Q plot of the bootstrap replicates. The order statistics of the replicates can be plotted against normal or chi-squared quantiles. In either case the expected line is also plotted. For the normal, this will have intercept mean(t) and slope sqrt(var(t)) while for the chi-squared it has intercept 0 and slope 1.

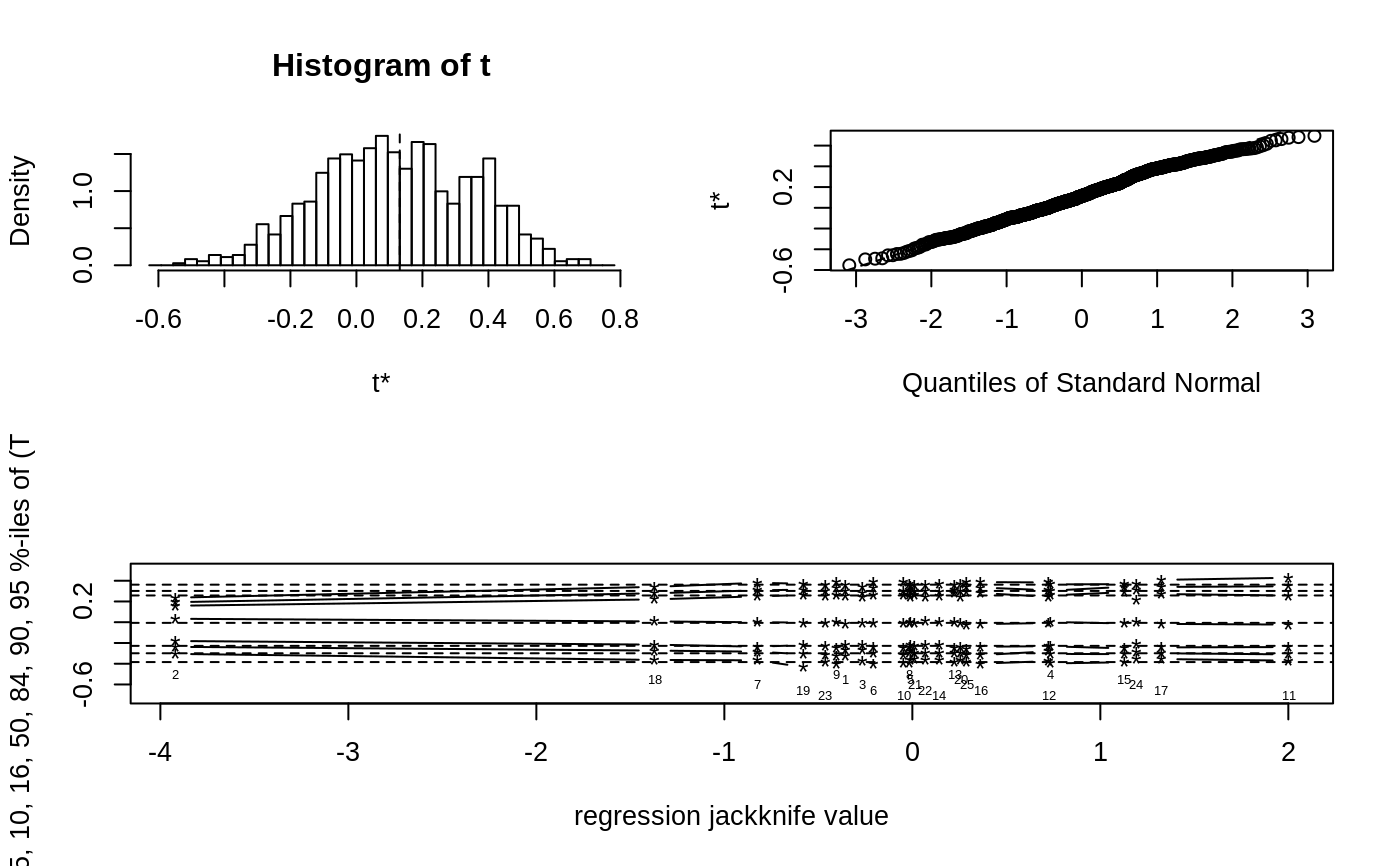
If jack is TRUE a third plot is produced beneath these two. That plot is the jackknife-after-bootstrap plot. This plot may only be requested when nonparametric simulation has been used. See jack.after.boot for further details of this plot.

Examples

# We fit an exponential model to the air-conditioning data and use
# that for a parametric bootstrap.  Then we look at plots of the
# resampled means.
air.rg <- function(data, mle) rexp(length(data), 1/mle)

air.boot <- boot(aircondit$hours, mean, R = 999, sim = "parametric",
                 ran.gen = air.rg, mle = mean(aircondit$hours))
plot(air.boot)

# In the difference of means example for the last two series of the 
# gravity data
grav1 <- gravity[as.numeric(gravity[, 2]) >= 7, ]
grav.fun <- function(dat, w) {
     strata <- tapply(dat[, 2], as.numeric(dat[, 2]))
     d <- dat[, 1]
     ns <- tabulate(strata)
     w <- w/tapply(w, strata, sum)[strata]
     mns <- as.vector(tapply(d * w, strata, sum)) # drop names
     mn2 <- tapply(d * d * w, strata, sum)
     s2hat <- sum((mn2 - mns^2)/ns)
     c(mns[2] - mns[1], s2hat)
}

grav.boot <- boot(grav1, grav.fun, R = 499, stype = "w", strata = grav1[, 2])
plot(grav.boot)
# now suppose we want to look at the studentized differences.
grav.z <- (grav.boot$t[, 1]-grav.boot$t0[1])/sqrt(grav.boot$t[, 2])
plot(grav.boot, t = grav.z, t0 = 0)

# In this example we look at the one of the partial correlations for the
# head dimensions in the dataset frets.
frets.fun <- function(data, i) {
    pcorr <- function(x) {
    #  Function to find the correlations and partial correlations between
    #  the four measurements.
         v <- cor(x)
         v.d <- diag(var(x))
         iv <- solve(v)
         iv.d <- sqrt(diag(iv))
         iv <- - diag(1/iv.d) %*% iv %*% diag(1/iv.d)
         q <- NULL
         n <- nrow(v)
         for (i in 1:(n-1))
              q <- rbind( q, c(v[i, 1:i], iv[i,(i+1):n]) )
         q <- rbind( q, v[n, ] )
         diag(q) <- round(diag(q))
         q
    }
    d <- data[i, ]
    v <- pcorr(d)
    c(v[1,], v[2,], v[3,], v[4,])
}
frets.boot <- boot(log(as.matrix(frets)),  frets.fun,  R = 999)
plot(frets.boot, index = 7, jack = TRUE, stinf = FALSE, useJ = FALSE)