Bivariate Cluster Plot (clusplot) Default Method

Creates a bivariate plot visualizing a partition (clustering) of the data. All observation are represented by points in the plot, using principal components or multidimensional scaling. Around each cluster an ellipse is drawn.

# S3 method for default
clusplot(x, clus, diss = FALSE,
          s.x.2d = mkCheckX(x, diss), stand = FALSE,
          lines = 2, shade = FALSE, color = FALSE,
          labels= 0, plotchar = TRUE,
          col.p = "dark green", col.txt = col.p,
          col.clus = if(color) c(2, 4, 6, 3) else 5, cex = 1, cex.txt = cex,
          span = TRUE,
          add = FALSE,
          xlim = NULL, ylim = NULL,
          main = paste("CLUSPLOT(", deparse(substitute(x)),")"),
          sub = paste("These two components explain",
             round(100 * var.dec, digits = 2), "% of the point variability."),
          xlab = "Component 1", ylab = "Component 2",
          verbose = getOption("verbose"),
          ...)

Arguments

x	matrix or data frame, or dissimilarity matrix, depending on the value of the diss argument. In case of a matrix (alike), each row corresponds to an observation, and each column corresponds to a variable. All variables must be numeric. Missing values (NAs) are allowed. They are replaced by the median of the corresponding variable. When some variables or some observations contain only missing values, the function stops with a warning message. In case of a dissimilarity matrix, x is the output of daisy or dist or a symmetric matrix. Also, a vector of length \(n*(n-1)/2\) is allowed (where \(n\) is the number of observations), and will be interpreted in the same way as the output of the above-mentioned functions. Missing values (NAs) are not allowed.
clus	a vector of length n representing a clustering of x. For each observation the vector lists the number or name of the cluster to which it has been assigned. clus is often the clustering component of the output of pam, fanny or clara.
diss	logical indicating if x will be considered as a dissimilarity matrix or a matrix of observations by variables (see x arugment above).
s.x.2d	a list with components named x (a \(n \times 2\) matrix; typically something like principal components of original data), labs and var.dec.
stand	logical flag: if true, then the representations of the n observations in the 2-dimensional plot are standardized.
lines	integer out of 0, 1, 2, used to obtain an idea of the distances between ellipses. The distance between two ellipses E1 and E2 is measured along the line connecting the centers \(m1\) and \(m2\) of the two ellipses. In case E1 and E2 overlap on the line through \(m1\) and \(m2\), no line is drawn. Otherwise, the result depends on the value of lines: If lines = 0, no distance lines will appear on the plot; lines = 1, the line segment between \(m1\) and \(m2\) is drawn; lines = 2, a line segment between the boundaries of E1 and E2 is drawn (along the line connecting \(m1\) and \(m2\)).
shade	logical flag: if TRUE, then the ellipses are shaded in relation to their density. The density is the number of points in the cluster divided by the area of the ellipse.
color	logical flag: if TRUE, then the ellipses are colored with respect to their density. With increasing density, the colors are light blue, light green, red and purple. To see these colors on the graphics device, an appropriate color scheme should be selected (we recommend a white background).
labels	integer code, currently one of 0,1,2,3,4 and 5. If labels= 0, no labels are placed in the plot; labels= 1, points and ellipses can be identified in the plot (see identify); labels= 2, all points and ellipses are labelled in the plot; labels= 3, only the points are labelled in the plot; labels= 4, only the ellipses are labelled in the plot. labels= 5, the ellipses are labelled in the plot, and points can be identified. The levels of the vector clus are taken as labels for the clusters. The labels of the points are the rownames of x if x is matrix like. Otherwise (diss = TRUE), x is a vector, point labels can be attached to x as a "Labels" attribute (attr(x,"Labels")), as is done for the output of daisy. A possible names attribute of clus will not be taken into account.
plotchar	logical flag: if TRUE, then the plotting symbols differ for points belonging to different clusters.
span	logical flag: if TRUE, then each cluster is represented by the ellipse with smallest area containing all its points. (This is a special case of the minimum volume ellipsoid.) If FALSE, the ellipse is based on the mean and covariance matrix of the same points. While this is faster to compute, it often yields a much larger ellipse. There are also some special cases: When a cluster consists of only one point, a tiny circle is drawn around it. When the points of a cluster fall on a straight line, span=FALSE draws a narrow ellipse around it and span=TRUE gives the exact line segment.
add	logical indicating if ellipses (and labels if labels is true) should be added to an already existing plot. If false, neither a title or sub title, see sub, is written.
col.p	color code(s) used for the observation points.
col.txt	color code(s) used for the labels (if labels >= 2).
col.clus	color code for the ellipses (and their labels); only one if color is false (as per default).
cex, cex.txt	character expansion (size), for the point symbols and point labels, respectively.
xlim, ylim	numeric vectors of length 2, giving the x- and y- ranges as in plot.default.
main	main title for the plot; by default, one is constructed.
sub	sub title for the plot; by default, one is constructed.
xlab, ylab	x- and y- axis labels for the plot, with defaults.
verbose	a logical indicating, if there should be extra diagnostic output; mainly for ‘debugging’.
...	Further graphical parameters may also be supplied, see par.

Value

An invisible list with components:

Distances

When lines is 1 or 2 we optain a k by k matrix (k is the number of clusters). The element in [i,j] is the distance between ellipse i and ellipse j.
If lines = 0, then the value of this component is NA.

Shading

A vector of length k (where k is the number of clusters), containing the amount of shading per cluster. Let y be a vector where element i is the ratio between the number of points in cluster i and the area of ellipse i. When the cluster i is a line segment, y[i] and the density of the cluster are set to NA. Let z be the sum of all the elements of y without the NAs. Then we put shading = y/z *37 + 3 .

Side Effects

a visual display of the clustering is plotted on the current graphics device.

Details

clusplot uses function calls princomp(*, cor = (ncol(x) > 2)) or cmdscale(*, add=TRUE), respectively, depending on diss being false or true. These functions are data reduction techniques to represent the data in a bivariate plot.

Ellipses are then drawn to indicate the clusters. The further layout of the plot is determined by the optional arguments.

Note

When we have 4 or fewer clusters, then the color=TRUE gives every cluster a different color. When there are more than 4 clusters, clusplot uses the function pam to cluster the densities into 4 groups such that ellipses with nearly the same density get the same color. col.clus specifies the colors used.

The col.p and col.txt arguments, added for R, are recycled to have length the number of observations. If col.p has more than one value, using color = TRUE can be confusing because of a mix of point and ellipse colors.

References

Pison, G., Struyf, A. and Rousseeuw, P.J. (1999) Displaying a Clustering with CLUSPLOT, Computational Statistics and Data Analysis, 30, 381--392.

Kaufman, L. and Rousseeuw, P.J. (1990). Finding Groups in Data: An Introduction to Cluster Analysis. Wiley, New York.

Struyf, A., Hubert, M. and Rousseeuw, P.J. (1997). Integrating Robust Clustering Techniques in S-PLUS, Computational Statistics and Data Analysis, 26, 17-37.

See also

princomp, cmdscale, pam, clara, daisy, par, identify, cov.mve, clusplot.partition.

Examples

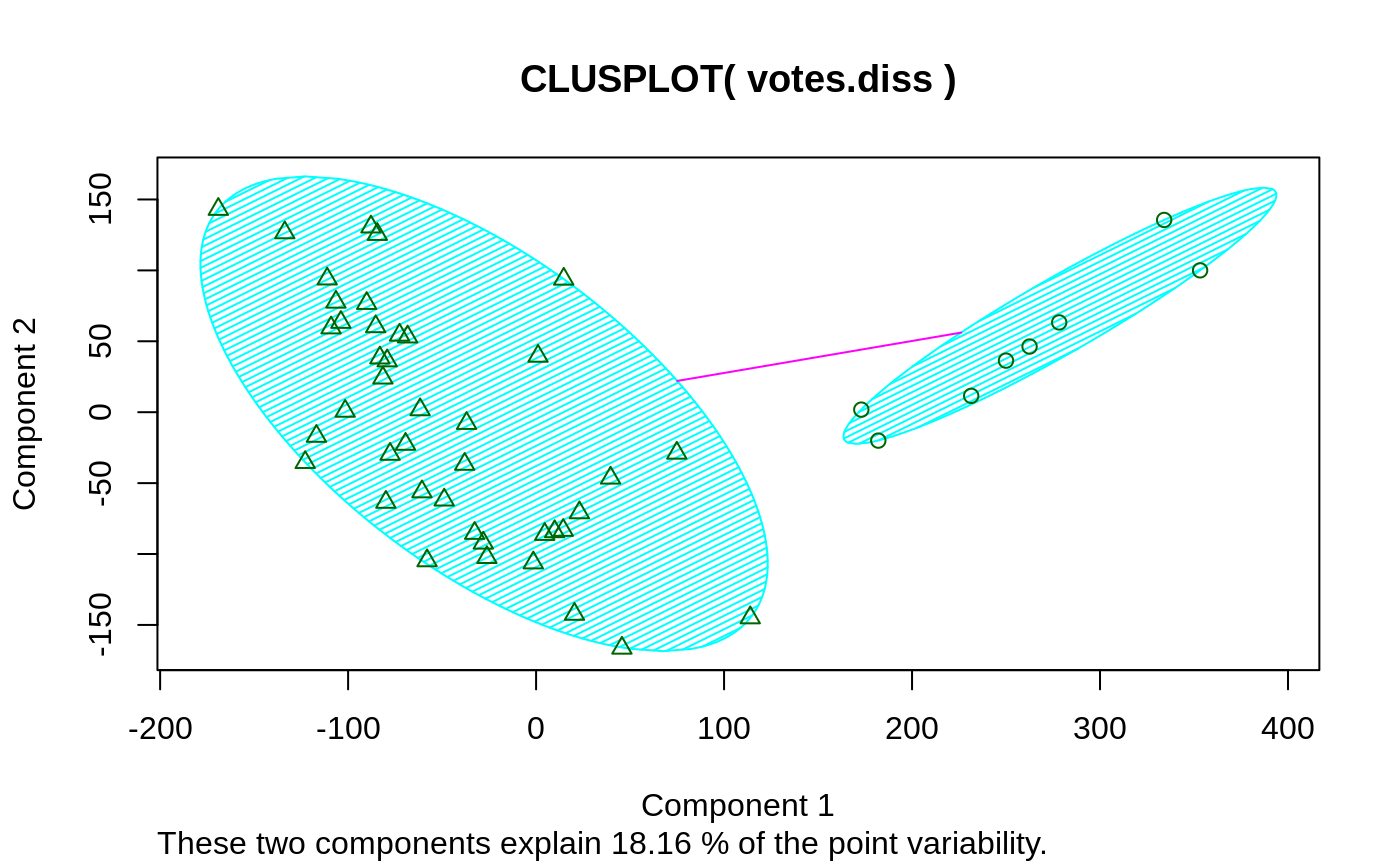
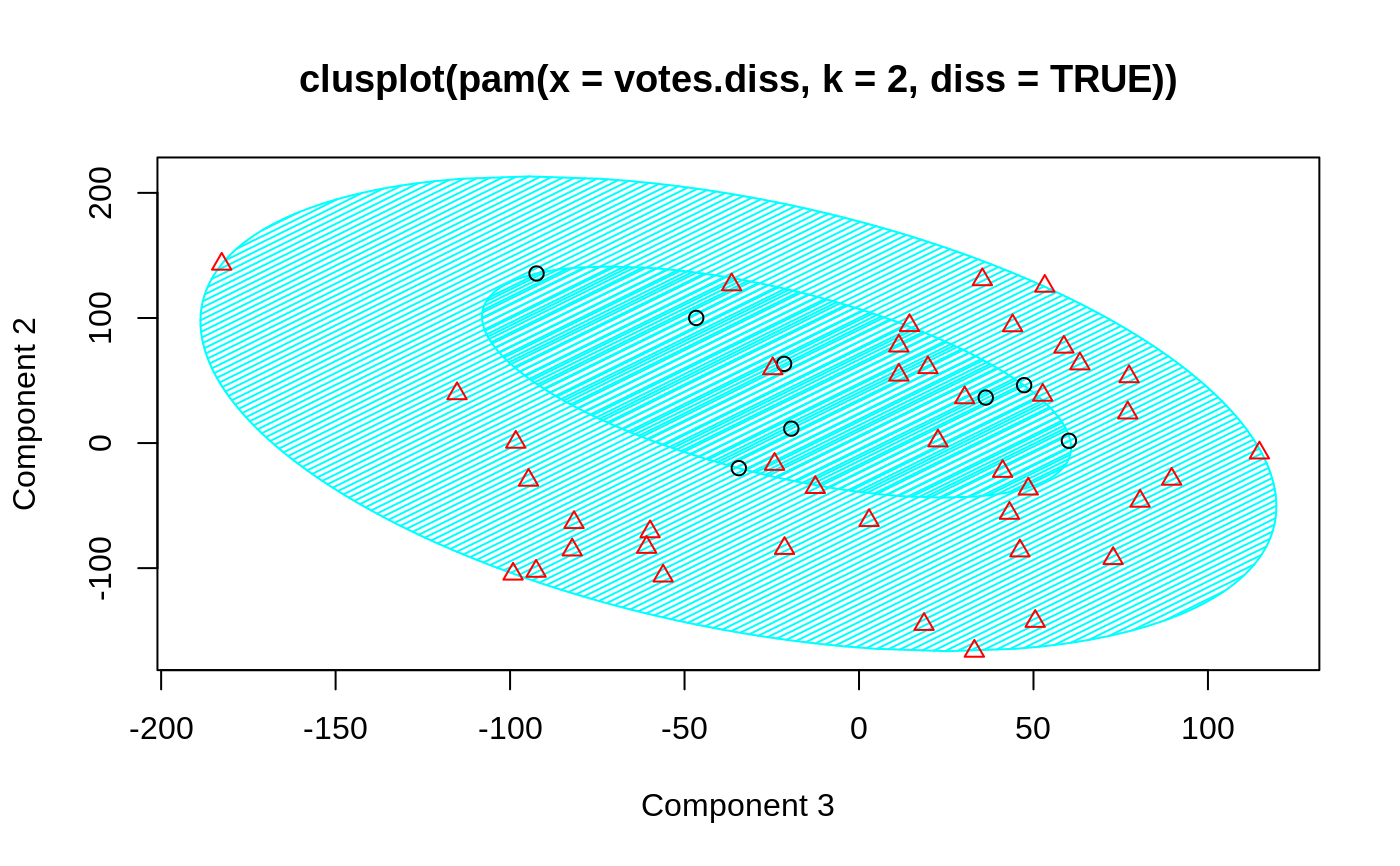
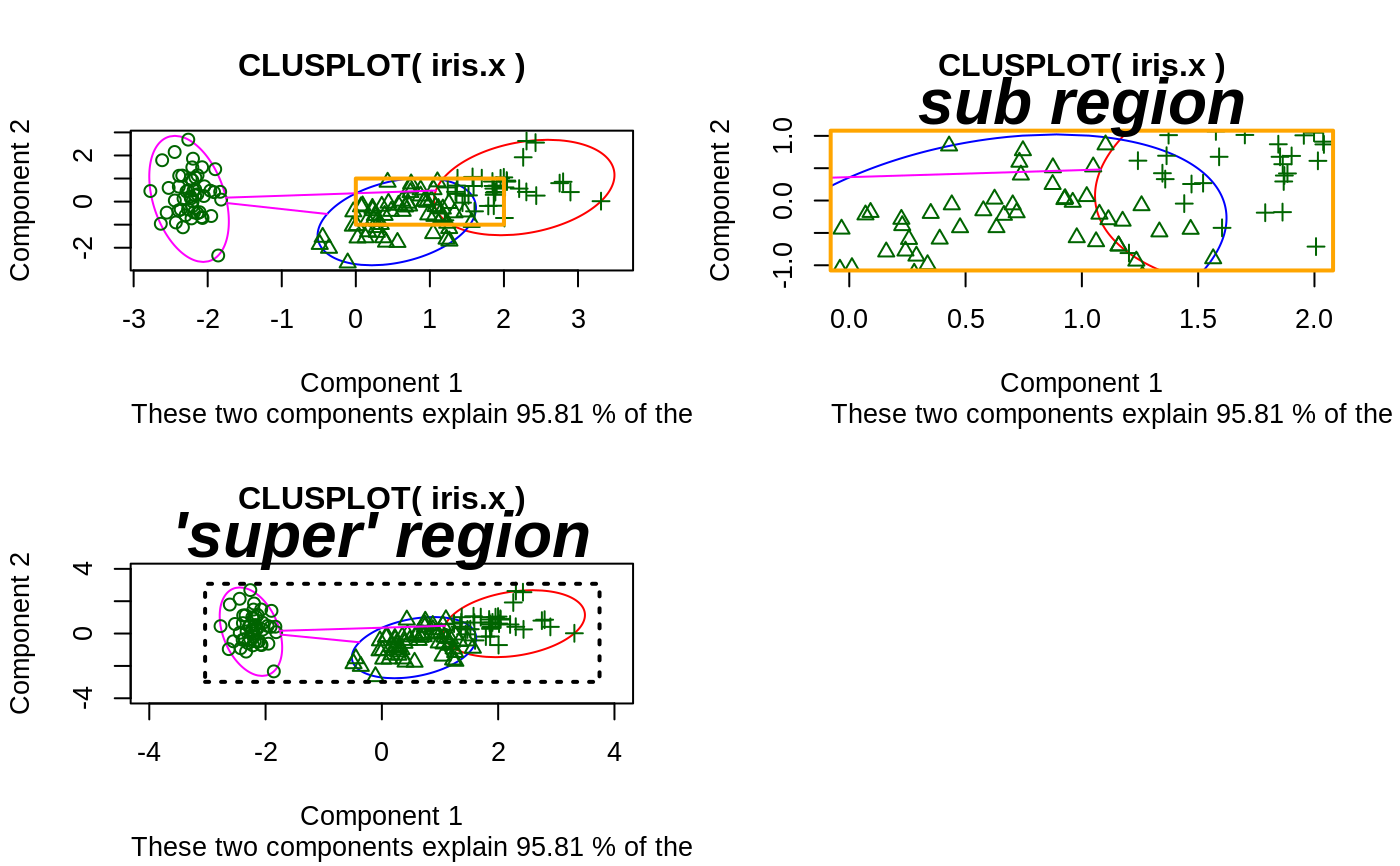
## plotting votes.diss(dissimilarity) in a bivariate plot and
## partitioning into 2 clusters
data(votes.repub)
votes.diss <- daisy(votes.repub)
pamv <- pam(votes.diss, 2, diss = TRUE)
clusplot(pamv, shade = TRUE)
## is the same as
votes.clus <- pamv$clustering
clusplot(votes.diss, votes.clus, diss = TRUE, shade = TRUE)
## Now look at components 3 and 2 instead of 1 and 2:
str(cMDS <- cmdscale(votes.diss, k=3, add=TRUE))
#> List of 5
#>  $ points: num [1:50, 1:3] 249.98 1.03 14.44 173.01 -37.99 ...
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : chr [1:50] "Alabama" "Alaska" "Arizona" "Arkansas" ...
#>   .. ..$ : NULL
#>  $ eig   : NULL
#>  $ x     : NULL
#>  $ ac    : num 420
#>  $ GOF   : num [1:2] 0.215 0.215
clusplot(pamv, s.x.2d = list(x=cMDS$points[, c(3,2)],
                             labs=rownames(votes.repub), var.dec=NA),
         shade = TRUE, col.p = votes.clus,
         sub="", xlab = "Component 3", ylab = "Component 2")

clusplot(pamv, col.p = votes.clus, labels = 4)# color points and label ellipses
# "simple" cheap ellipses: larger than minimum volume:
# here they are *added* to the previous plot:
clusplot(pamv, span = FALSE, add = TRUE, col.clus = "midnightblue")

## Setting a small *label* size:
clusplot(votes.diss, votes.clus, diss = TRUE, labels = 3, cex.txt = 0.6)

if(dev.interactive()) { #  uses identify() *interactively* :
  clusplot(votes.diss, votes.clus, diss = TRUE, shade = TRUE, labels = 1)
  clusplot(votes.diss, votes.clus, diss = TRUE, labels = 5)# ident. only points
}

## plotting iris (data frame) in a 2-dimensional plot and partitioning
## into 3 clusters.
data(iris)
iris.x <- iris[, 1:4]
cl3 <- pam(iris.x, 3)$clustering
op <- par(mfrow= c(2,2))
clusplot(iris.x, cl3, color = TRUE)
U <- par("usr")
## zoom in :
rect(0,-1, 2,1, border = "orange", lwd=2)
clusplot(iris.x, cl3, color = TRUE, xlim = c(0,2), ylim = c(-1,1))
box(col="orange",lwd=2); mtext("sub region", font = 4, cex = 2)
##  or zoom out :
clusplot(iris.x, cl3, color = TRUE, xlim = c(-4,4), ylim = c(-4,4))
mtext("'super' region", font = 4, cex = 2)
rect(U[1],U[3], U[2],U[4], lwd=2, lty = 3)

# reset graphics
par(op)