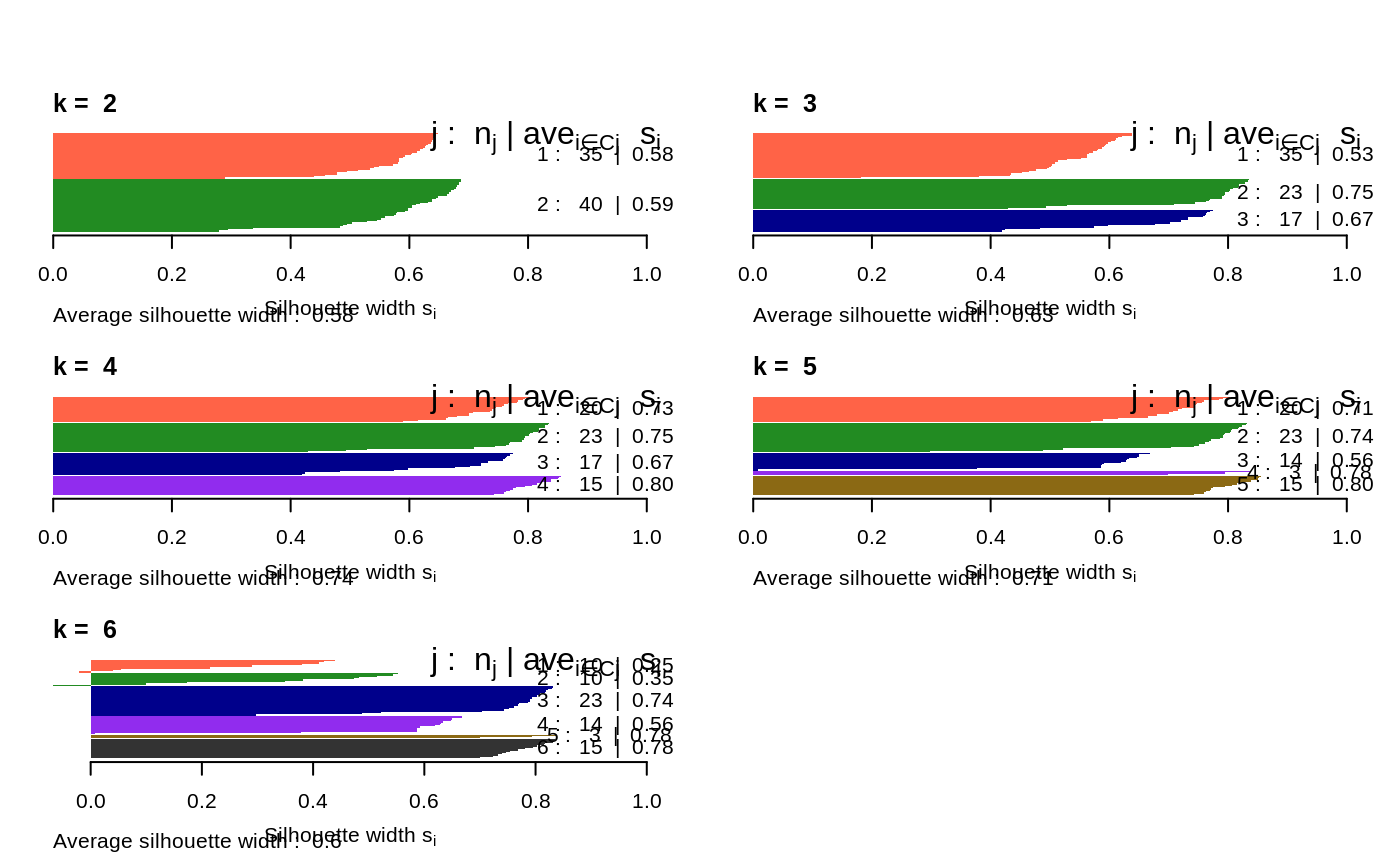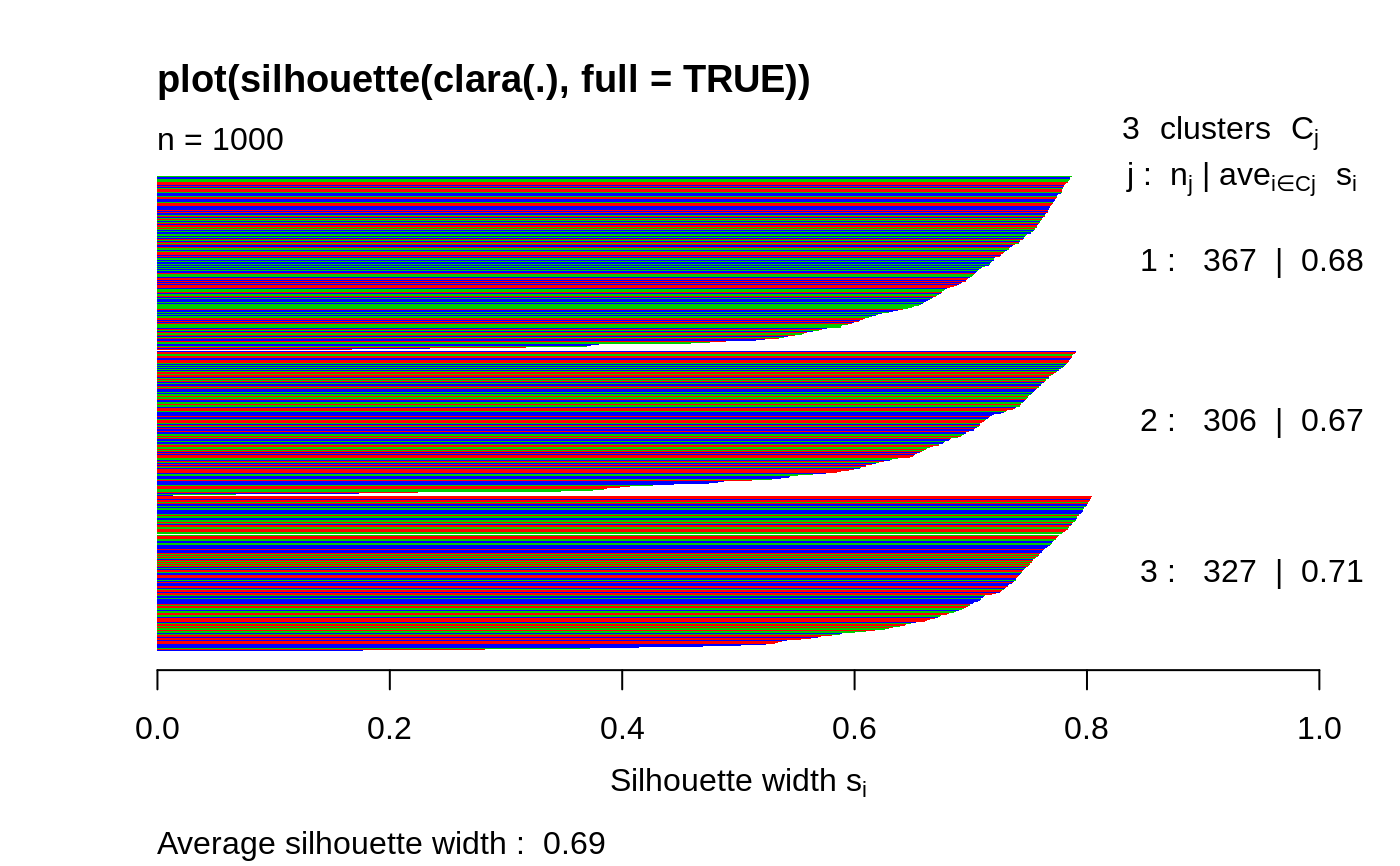Compute or Extract Silhouette Information from Clustering

Compute silhouette information according to a given clustering in \(k\) clusters.

silhouette(x, ...)
# S3 method for default
silhouette  (x, dist, dmatrix, ...)
# S3 method for partition
silhouette(x, ...)
# S3 method for clara
silhouette(x, full = FALSE, ...)

sortSilhouette(object, ...)
# S3 method for silhouette
summary(object, FUN = mean, ...)
# S3 method for silhouette
plot(x, nmax.lab = 40, max.strlen = 5,
     main = NULL, sub = NULL, xlab = expression("Silhouette width "* s[i]),
     col = "gray",  do.col.sort = length(col) > 1, border = 0,
     cex.names = par("cex.axis"), do.n.k = TRUE, do.clus.stat = TRUE, ...)

Arguments

x	an object of appropriate class; for the default method an integer vector with \(k\) different integer cluster codes or a list with such an x$clustering component. Note that silhouette statistics are only defined if \(2 \le k \le n-1\).
dist	a dissimilarity object inheriting from class dist or coercible to one. If not specified, dmatrix must be.
dmatrix	a symmetric dissimilarity matrix (\(n \times n\)), specified instead of dist, which can be more efficient.
full	logical specifying if a full silhouette should be computed for clara object. Note that this requires \(O(n^2)\) memory, since the full dissimilarity (see daisy) is needed internally.
object	an object of class silhouette.
...	further arguments passed to and from methods.
FUN	function used to summarize silhouette widths.
nmax.lab	integer indicating the number of labels which is considered too large for single-name labeling the silhouette plot.
max.strlen	positive integer giving the length to which strings are truncated in silhouette plot labeling.
main, sub, xlab	arguments to title; have a sensible non-NULL default here.
col, border, cex.names	arguments passed barplot(); note that the default used to be col = heat.colors(n), border = par("fg") instead. col can also be a color vector of length \(k\) for clusterwise coloring, see also do.col.sort:
do.col.sort	logical indicating if the colors col should be sorted “along” the silhouette; this is useful for casewise or clusterwise coloring.
do.n.k	logical indicating if \(n\) and \(k\) “title text” should be written.
do.clus.stat	logical indicating if cluster size and averages should be written right to the silhouettes.

Details

For each observation i, the silhouette width \(s(i)\) is defined as follows:
Put a(i) = average dissimilarity between i and all other points of the cluster to which i belongs (if i is the only observation in its cluster, \(s(i) := 0\) without further calculations). For all other clusters C, put \(d(i,C)\) = average dissimilarity of i to all observations of C. The smallest of these \(d(i,C)\) is \(b(i) := \min_C d(i,C)\), and can be seen as the dissimilarity between i and its “neighbor” cluster, i.e., the nearest one to which it does not belong. Finally, $$s(i) := \frac{b(i) - a(i) }{max(a(i), b(i))}.$$

silhouette.default() is now based on C code donated by Romain Francois (the R version being still available as cluster:::silhouette.default.R).

Observations with a large \(s(i)\) (almost 1) are very well clustered, a small \(s(i)\) (around 0) means that the observation lies between two clusters, and observations with a negative \(s(i)\) are probably placed in the wrong cluster.

Note

While silhouette() is intrinsic to the partition clusterings, and hence has a (trivial) method for these, it is straightforward to get silhouettes from hierarchical clusterings from silhouette.default() with cutree() and distance as input.

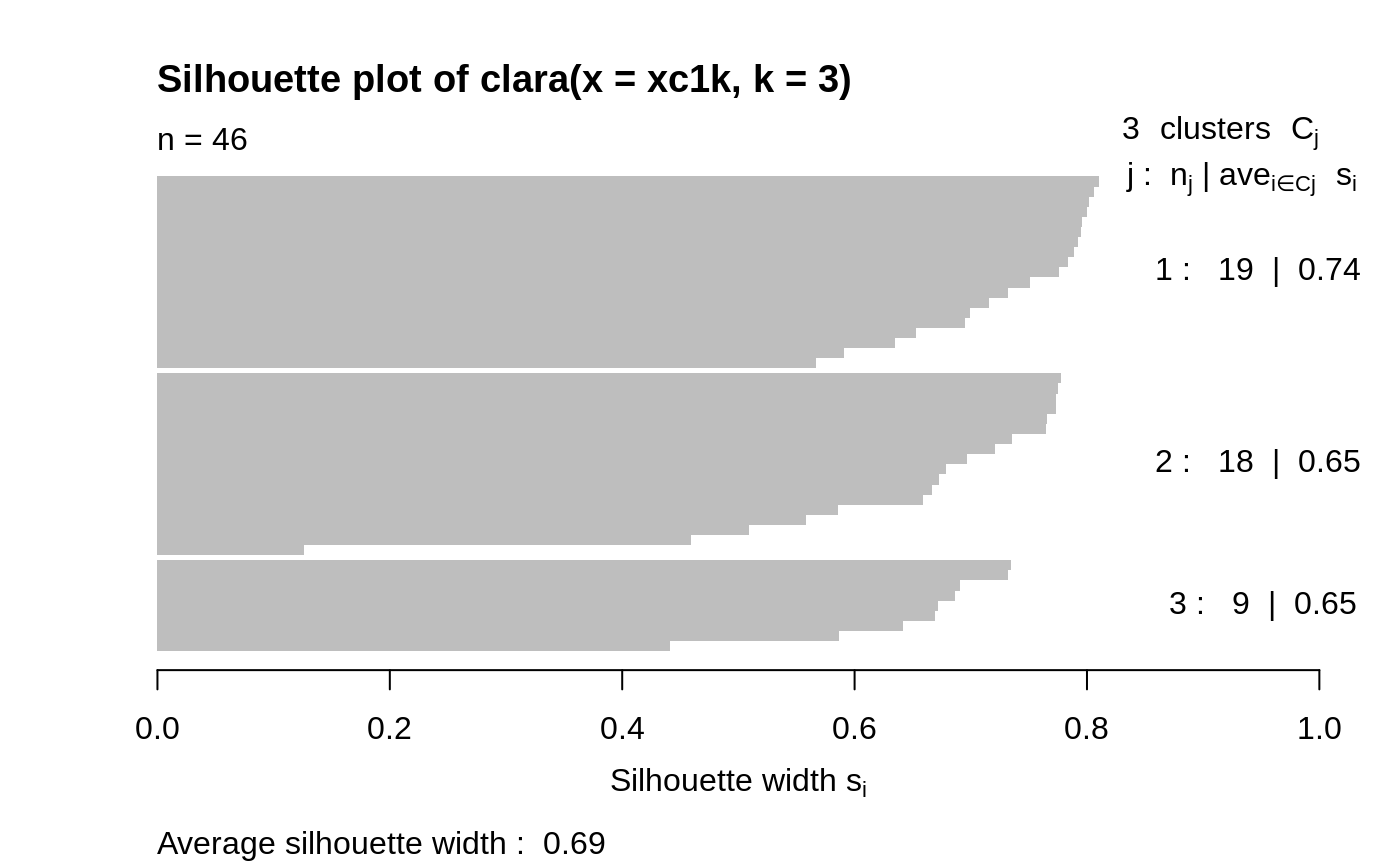
By default, for clara() partitions, the silhouette is just for the best random subset used. Use full = TRUE to compute (and later possibly plot) the full silhouette.

Value

silhouette() returns an object, sil, of class silhouette which is an \(n \times 3\) matrix with attributes. For each observation i, sil[i,] contains the cluster to which i belongs as well as the neighbor cluster of i (the cluster, not containing i, for which the average dissimilarity between its observations and i is minimal), and the silhouette width \(s(i)\) of the observation. The colnames correspondingly are c("cluster", "neighbor", "sil_width").

summary(sil) returns an object of class summary.silhouette, a list with components

si.summary:

numerical summary of the individual silhouette widths \(s(i)\).

clus.avg.widths:

numeric (rank 1) array of clusterwise means of silhouette widths where mean = FUN is used.

avg.width:

the total mean FUN(s) where s are the individual silhouette widths.

clus.sizes:

table of the \(k\) cluster sizes.

call:

if available, the call creating sil.

Ordered:

logical identical to attr(sil, "Ordered"), see below.

sortSilhouette(sil) orders the rows of sil as in the silhouette plot, by cluster (increasingly) and decreasing silhouette width \(s(i)\).
attr(sil, "Ordered") is a logical indicating if sil is ordered as by sortSilhouette(). In that case, rownames(sil) will contain case labels or numbers, and
attr(sil, "iOrd") the ordering index vector.

References

Rousseeuw, P.J. (1987) Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math., 20, 53--65.

chapter 2 of Kaufman and Rousseeuw (1990), see the references in plot.agnes.

See also

partition.object, plot.partition.

Examples

data(ruspini)
pr4 <- pam(ruspini, 4)
str(si <- silhouette(pr4))
#>  'silhouette' num [1:75, 1:3] 1 1 1 1 1 1 1 1 1 1 ...
#>  - attr(*, "dimnames")=List of 2
#>   ..$ : chr [1:75] "10" "6" "9" "11" ...
#>   ..$ : chr [1:3] "cluster" "neighbor" "sil_width"
#>  - attr(*, "Ordered")= logi TRUE
#>  - attr(*, "call")= language pam(x = ruspini, k = 4)
(ssi <- summary(si))
#> Silhouette of 75 units in 4 clusters from pam(x = ruspini, k = 4) :
#>  Cluster sizes and average silhouette widths:
#>        20        23        17        15 
#> 0.7262347 0.7548344 0.6691154 0.8042285 
#> Individual silhouette widths:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>  0.4196  0.7145  0.7642  0.7377  0.7984  0.8549 
plot(si) # silhouette plot
plot(si, col = c("red", "green", "blue", "purple"))# with cluster-wise coloring

si2 <- silhouette(pr4$clustering, dist(ruspini, "canberra"))
summary(si2) # has small values: "canberra"'s fault
#> Silhouette of 75 units in 4 clusters from silhouette.default(x = pr4$clustering, dist = dist(ruspini, "canberra")) :
#>  Cluster sizes and average silhouette widths:
#>        20        23        17        15 
#> 0.4704136 0.6699338 0.7339873 0.6623204 
#> Individual silhouette widths:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#> 0.07951 0.55135 0.67585 0.62972 0.75332 0.82071 
plot(si2, nmax= 80, cex.names=0.6)

op <- par(mfrow= c(3,2), oma= c(0,0, 3, 0),
          mgp= c(1.6,.8,0), mar= .1+c(4,2,2,2))
for(k in 2:6)
   plot(silhouette(pam(ruspini, k=k)), main = paste("k = ",k), do.n.k=FALSE)
mtext("PAM(Ruspini) as in Kaufman & Rousseeuw, p.101",
      outer = TRUE, font = par("font.main"), cex = par("cex.main")); frame()

## the same with cluster-wise colours:
c6 <- c("tomato", "forest green", "dark blue", "purple2", "goldenrod4", "gray20")
for(k in 2:6)
   plot(silhouette(pam(ruspini, k=k)), main = paste("k = ",k), do.n.k=FALSE,
        col = c6[1:k])
par(op)

## clara(): standard silhouette is just for the best random subset
data(xclara)
set.seed(7)
str(xc1k <- xclara[ sample(nrow(xclara), size = 1000) ,]) # rownames == indices
#> 'data.frame':	1000 obs. of  2 variables:
#>  $ V1: num  44.6 11.2 71.6 17.6 77.5 ...
#>  $ V2: num  78.78 27.96 -26.88 69.15 -7.26 ...
cl3 <- clara(xc1k, 3)
plot(silhouette(cl3))# only of the "best" subset of 46
## The full silhouette: internally needs large (36 MB) dist object:
sf <- silhouette(cl3, full = TRUE) ## this is the same as
s.full <- silhouette(cl3$clustering, daisy(xc1k))
stopifnot(all.equal(sf, s.full, check.attributes = FALSE, tolerance = 0))
## color dependent on original "3 groups of each 1000": % __FIXME ??__
plot(sf, col = 2+ as.integer(names(cl3$clustering) ) %/% 1000,
     main ="plot(silhouette(clara(.), full = TRUE))")

## Silhouette for a hierarchical clustering:
ar <- agnes(ruspini)
si3 <- silhouette(cutree(ar, k = 5), # k = 4 gave the same as pam() above
                   daisy(ruspini))
plot(si3, nmax = 80, cex.names = 0.5)
## 2 groups: Agnes() wasn't too good:
si4 <- silhouette(cutree(ar, k = 2), daisy(ruspini))
plot(si4, nmax = 80, cex.names = 0.5)