Summary Method for 'clara' Objects
summary.clara.RdReturns (and prints) a summary list for a clara object.
Printing gives more output than the corresponding
print.clara method.
# S3 method for clara summary(object, ...) # S3 method for summary.clara print(x, ...)
Arguments
| x, object | a |
|---|---|
| ... | potential further arguments (require by generic). |
See also
Examples
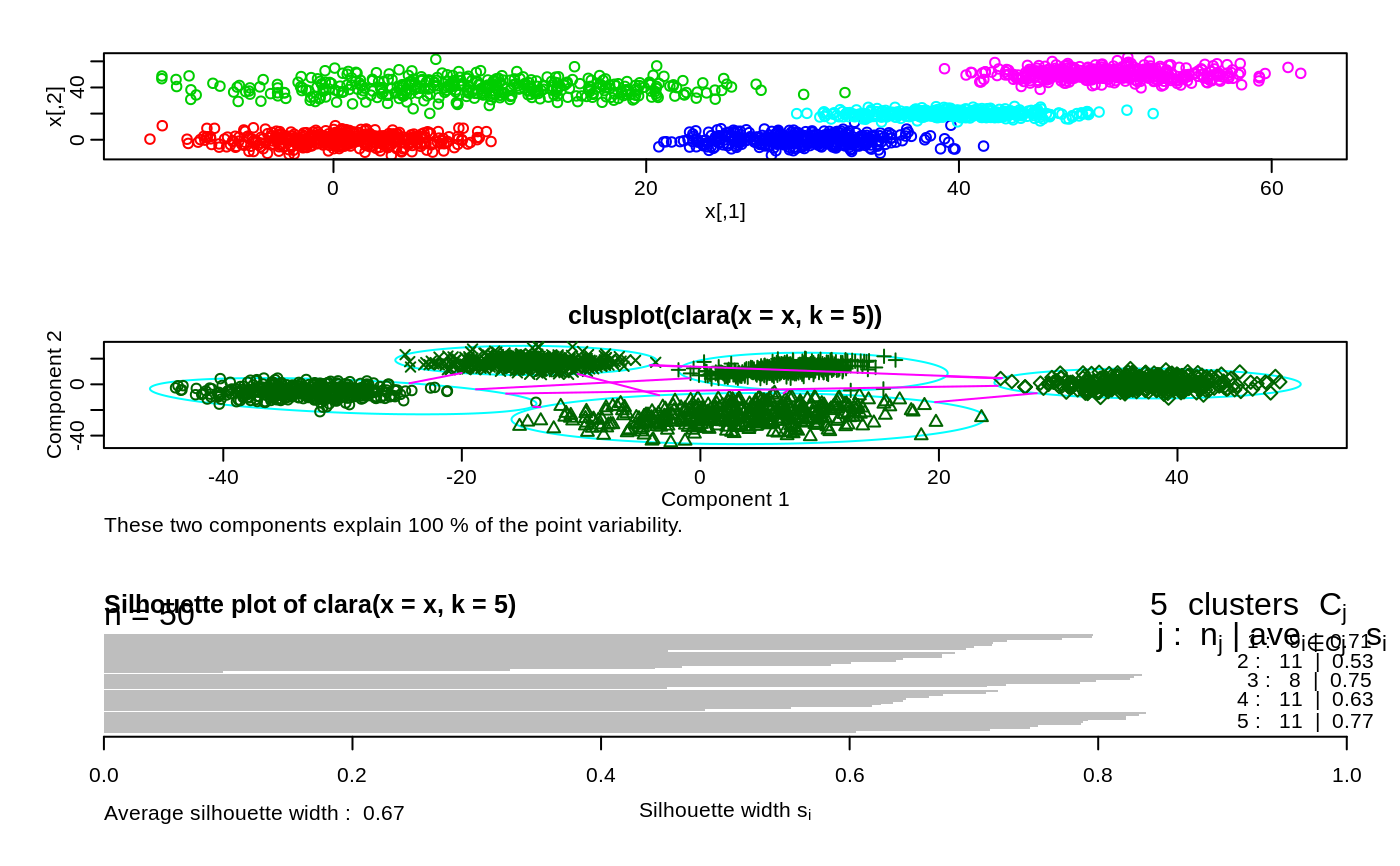
## generate 2000 objects, divided into 5 clusters. set.seed(47) x <- rbind(cbind(rnorm(400, 0,4), rnorm(400, 0,4)), cbind(rnorm(400,10,8), rnorm(400,40,6)), cbind(rnorm(400,30,4), rnorm(400, 0,4)), cbind(rnorm(400,40,4), rnorm(400,20,2)), cbind(rnorm(400,50,4), rnorm(400,50,4)) ) clx5 <- clara(x, 5) ## Mis'classification' table: table(rep(1:5, rep(400,5)), clx5$clust) # -> 1 "error"#> #> 1 2 3 4 5 #> 1 400 0 0 0 0 #> 2 1 397 2 0 0 #> 3 0 0 2 398 0 #> 4 0 0 400 0 0 #> 5 0 0 0 0 400summary(clx5)#> Object of class 'clara' from call: #> clara(x = x, k = 5) #> Medoids: #> [,1] [,2] #> [1,] -0.1035906 1.171950 #> [2,] 9.9499760 39.951186 #> [3,] 39.4474719 19.039427 #> [4,] 29.4759812 1.358166 #> [5,] 51.6823589 50.852512 #> Objective function: 5.718409 #> Numerical information per cluster: #> size max_diss av_diss isolation #> [1,] 401 19.97700 5.386022 0.6753513 #> [2,] 397 22.69885 8.906811 0.6277678 #> [3,] 404 18.31257 4.074241 0.9021325 #> [4,] 398 13.60096 4.858041 0.6700241 #> [5,] 400 13.90904 5.403812 0.4080733 #> Average silhouette width per cluster: #> [1] 0.7072538 0.5300758 0.7454078 0.6335300 0.7723767 #> Average silhouette width of best sample: 0.6724871 #> #> Best sample: #> [1] 10 50 186 300 322 349 376 378 382 415 450 484 523 615 638 #> [16] 673 683 763 780 799 820 841 864 873 874 887 926 1011 1017 1032 #> [31] 1056 1093 1214 1225 1272 1467 1494 1554 1570 1602 1713 1729 1753 1768 1818 #> [46] 1857 1895 1907 1934 1984 #> Clustering vector: #> [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 #> [38] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 #> [75] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 #> [112] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 #> [149] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 #> [186] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 #> [223] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 #> [260] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 #> [297] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 #> [334] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 #> [371] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 #> [408] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 #> [445] 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 #> [482] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 #> [519] 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 #> [556] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 #> [593] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 #> [630] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 #> [667] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 #> [704] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 #> [741] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 #> [778] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 4 4 4 4 4 4 4 4 4 4 4 4 4 4 #> [815] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 #> [852] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 3 4 #> [889] 4 4 4 4 4 4 4 4 4 4 4 4 4 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 #> [926] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 #> [963] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 #> [1000] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 #> [1037] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 #> [1074] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 #> [1111] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 #> [1148] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 #> [1185] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 #> [1222] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 #> [1259] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 #> [1296] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 #> [1333] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 #> [1370] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 #> [1407] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 #> [1444] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 #> [1481] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 #> [1518] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 #> [1555] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 #> [1592] 3 3 3 3 3 3 3 3 3 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 #> [1629] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 #> [1666] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 #> [1703] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 #> [1740] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 #> [1777] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 #> [1814] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 #> [1851] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 #> [1888] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 #> [1925] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 #> [1962] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 #> [1999] 5 5 #> #> Silhouette plot information for best sample: #> cluster neighbor sil_width #> 186 1 4 0.79556048 #> 376 1 4 0.79536776 #> 382 1 4 0.77049836 #> 322 1 4 0.72622987 #> 378 1 4 0.71528949 #> 300 1 4 0.71457724 #> 10 1 4 0.70035557 #> 50 1 4 0.69376464 #> 349 1 4 0.45364060 #> 638 2 3 0.68460064 #> 799 2 1 0.67412068 #> 615 2 1 0.67411646 #> 780 2 1 0.64309460 #> 450 2 3 0.63739841 #> 763 2 1 0.60137941 #> 484 2 5 0.58470680 #> 673 2 1 0.46544761 #> 415 2 3 0.44374622 #> 683 2 5 0.32679127 #> 523 2 3 0.09543198 #> 1214 3 4 0.83525228 #> 1225 3 4 0.82861718 #> 1494 3 4 0.82594085 #> 1467 3 4 0.79812526 #> 1570 3 4 0.78556940 #> 1554 3 4 0.72597072 #> 1272 3 4 0.71036496 #> 887 3 4 0.45342176 #> 864 4 3 0.71911350 #> 1093 4 3 0.70970985 #> 1011 4 3 0.67477005 #> 874 4 3 0.66351496 #> 1056 4 3 0.64502727 #> 820 4 3 0.64288797 #> 873 4 3 0.63456421 #> 1017 4 1 0.62532035 #> 926 4 1 0.61762610 #> 841 4 1 0.55247046 #> 1032 4 3 0.48382581 #> 1984 5 3 0.83811926 #> 1895 5 3 0.83276945 #> 1934 5 3 0.82244446 #> 1818 5 3 0.82210143 #> 1857 5 3 0.79188309 #> 1713 5 3 0.78758559 #> 1729 5 3 0.78583419 #> 1768 5 3 0.75181843 #> 1602 5 2 0.74495873 #> 1753 5 3 0.71331435 #> 1907 5 3 0.60531502 #> #> 1225 dissimilarities, summarized : #> Min. 1st Qu. Median Mean 3rd Qu. Max. #> 0.2376 23.0540 36.8570 36.2280 48.8530 82.1740 #> Metric : euclidean #> Number of objects : 50 #> #> Available components: #> [1] "sample" "medoids" "i.med" "clustering" "objective" #> [6] "clusinfo" "diss" "call" "silinfo" "data"## Graphically: par(mfrow = c(3,1), mgp = c(1.5, 0.6, 0), mar = par("mar") - c(0,0,2,0)) plot(x, col = rep(2:6, rep(400,5))) plot(clx5)