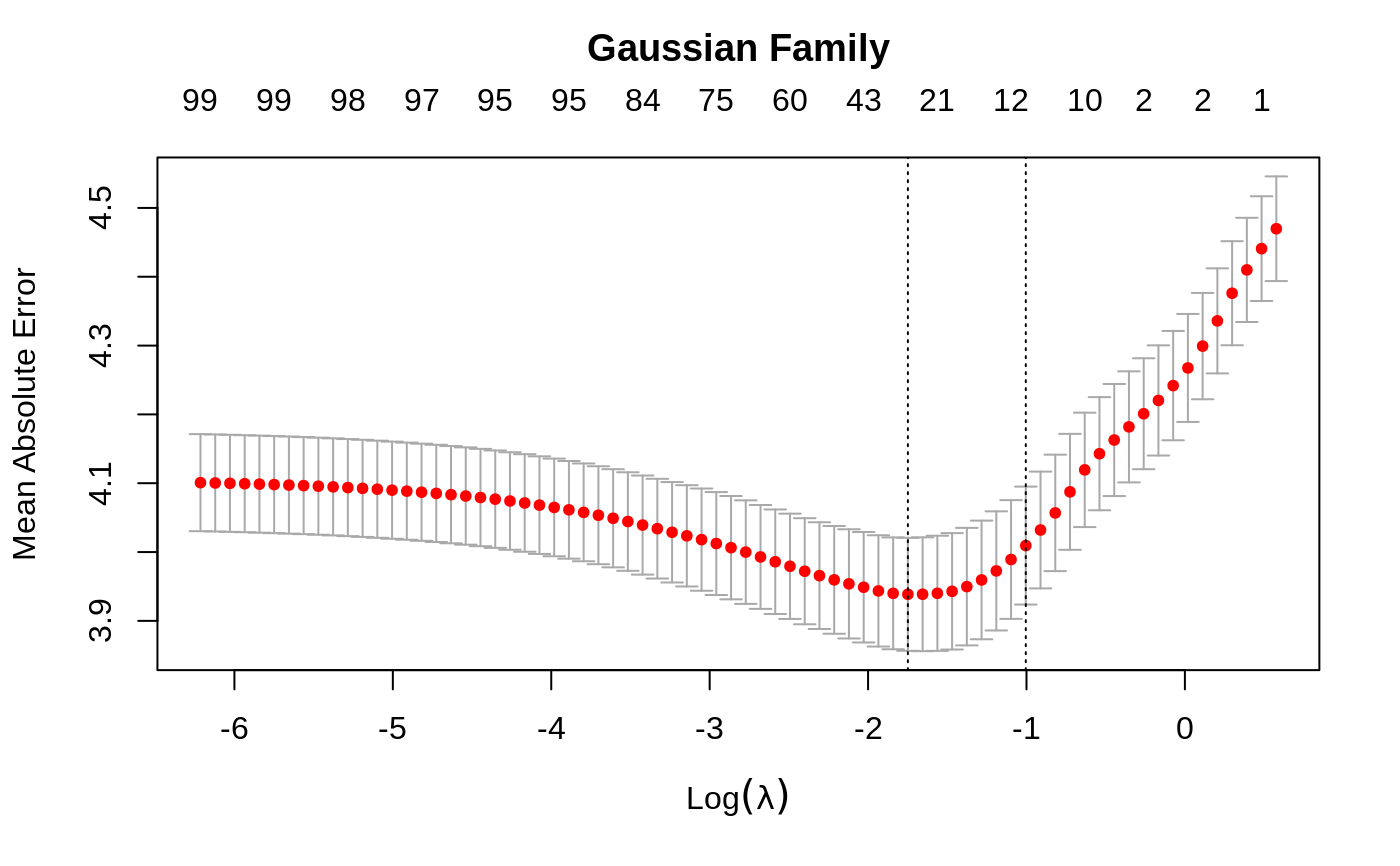
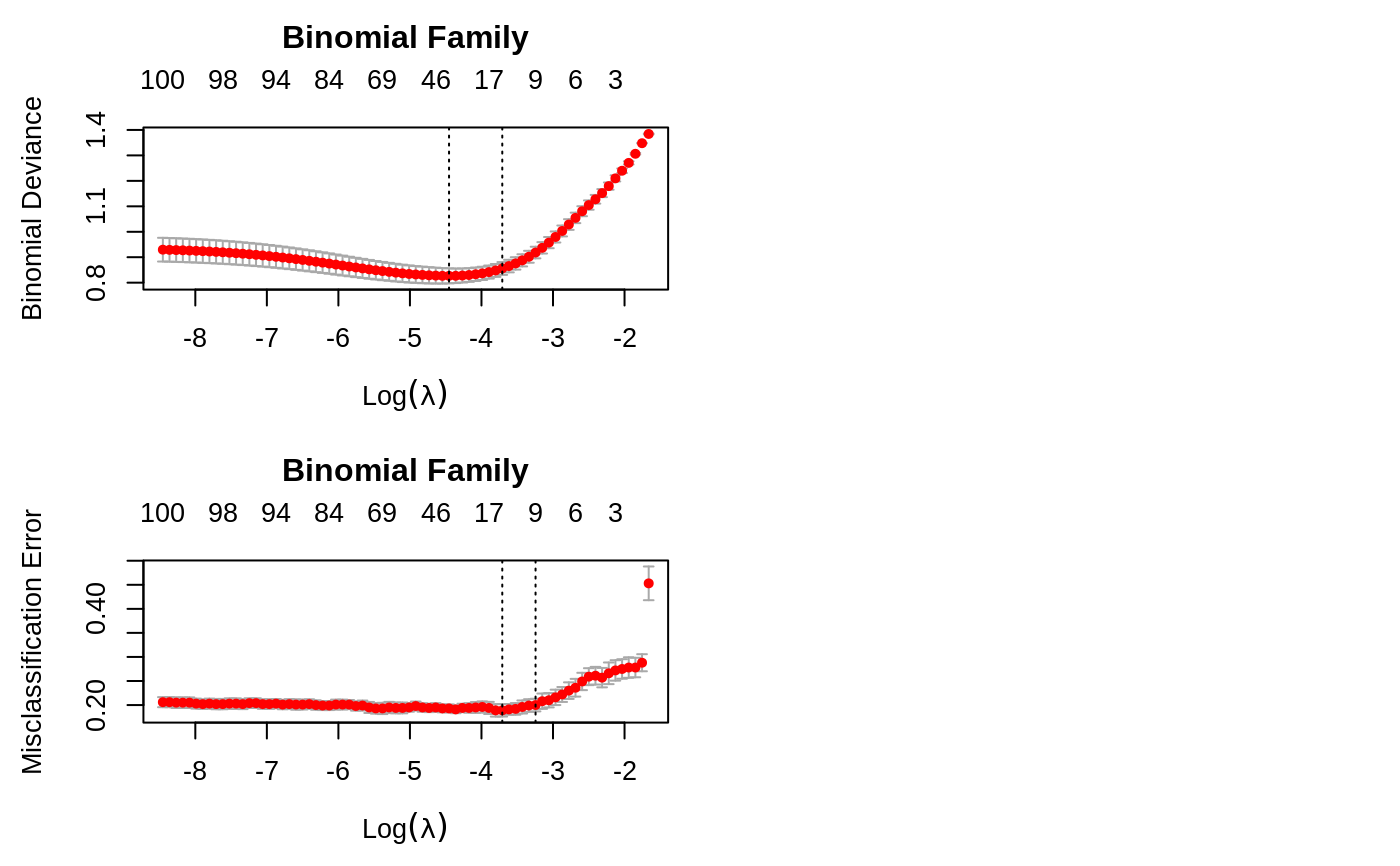
Cross-validation for glmnet

Does k-fold cross-validation for glmnet, produces a plot, and returns a value for lambda (and gamma if relax=TRUE)

cv.glmnet(x, y, weights = NULL, offset = NULL, lambda = NULL,
  type.measure = c("default", "mse", "deviance", "class", "auc", "mae",
  "C"), nfolds = 10, foldid = NULL, alignment = c("lambda",
  "fraction"), grouped = TRUE, keep = FALSE, parallel = FALSE,
  gamma = c(0, 0.25, 0.5, 0.75, 1), relax = FALSE, trace.it = 0, ...)

Arguments

x	x matrix as in glmnet.
y	response y as in glmnet.
weights	Observation weights; defaults to 1 per observation
offset	Offset vector (matrix) as in glmnet
lambda	Optional user-supplied lambda sequence; default is NULL, and glmnet chooses its own sequence
type.measure	loss to use for cross-validation. Currently five options, not all available for all models. The default is type.measure="deviance", which uses squared-error for gaussian models (a.k.a type.measure="mse" there), deviance for logistic and poisson regression, and partial-likelihood for the Cox model. type.measure="class" applies to binomial and multinomial logistic regression only, and gives misclassification error. type.measure="auc" is for two-class logistic regression only, and gives area under the ROC curve. type.measure="mse" or type.measure="mae" (mean absolute error) can be used by all models except the "cox"; they measure the deviation from the fitted mean to the response. type.measure="C" is Harrel's concordance measure, only available for cox models.
nfolds	number of folds - default is 10. Although nfolds can be as large as the sample size (leave-one-out CV), it is not recommended for large datasets. Smallest value allowable is nfolds=3
foldid	an optional vector of values between 1 and nfold identifying what fold each observation is in. If supplied, nfold can be missing.
alignment	This is an experimental argument, designed to fix the problems users were having with CV, with possible values "lambda" (the default) else "fraction". With "lambda" the lambda values from the master fit (on all the data) are used to line up the predictions from each of the folds. In some cases this can give strange values, since the effective lambda values in each fold could be quite different. With "fraction" we line up the predictions in each fold according to the fraction of progress along the regularization. If in the call a lambda argument is also provided, alignment="fraction" is ignored (with a warning).
grouped	This is an experimental argument, with default TRUE, and can be ignored by most users. For all models except the "cox", this refers to computing nfolds separate statistics, and then using their mean and estimated standard error to describe the CV curve. If grouped=FALSE, an error matrix is built up at the observation level from the predictions from the nfold fits, and then summarized (does not apply to type.measure="auc"). For the "cox" family, grouped=TRUE obtains the CV partial likelihood for the Kth fold by subtraction; by subtracting the log partial likelihood evaluated on the full dataset from that evaluated on the on the (K-1)/K dataset. This makes more efficient use of risk sets. With grouped=FALSE the log partial likelihood is computed only on the Kth fold
keep	If keep=TRUE, a prevalidated array is returned containing fitted values for each observation and each value of lambda. This means these fits are computed with this observation and the rest of its fold omitted. The folid vector is also returned. Default is keep=FALSE. If relax=TRUE, then a list of such arrays is returned, one for each value of 'gamma'. Note: if the value 'gamma=1' is omitted, this case is included in the list since it corresponds to the original 'glmnet' fit.
parallel	If TRUE, use parallel foreach to fit each fold. Must register parallel before hand, such as doMC or others. See the example below.
gamma	The values of the parameter for mixing the relaxed fit with the regularized fit, between 0 and 1; default is gamma = c(0, 0.25, 0.5, 0.75, 1)
relax	If TRUE, then CV is done with respect to the mixing parameter gamma as well as lambda. Default is relax=FALSE
trace.it	If trace.it=1, then progress bars are displayed; useful for big models that take a long time to fit. Limited tracing if parallel=TRUE
...	Other arguments that can be passed to glmnet

Value

an object of class "cv.glmnet" is returned, which is a list with the ingredients of the cross-validation fit. If the object was created with relax=TRUE then this class has a prefix class of "cv.relaxed".

lambda

the values of lambda used in the fits.

cvm

The mean cross-validated error - a vector of length length(lambda).

cvsd

estimate of standard error of cvm.

cvup

upper curve = cvm+cvsd.

cvlo

lower curve = cvm-cvsd.

nzero

number of non-zero coefficients at each lambda.

name

a text string indicating type of measure (for plotting purposes).

glmnet.fit

a fitted glmnet object for the full data.

lambda.min

value of lambda that gives minimum cvm.

lambda.1se

largest value of lambda such that error is within 1 standard error of the minimum.

fit.preval

if keep=TRUE, this is the array of prevalidated fits. Some entries can be NA, if that and subsequent values of lambda are not reached for that fold

foldid

if keep=TRUE, the fold assignments used

relaxed

if relax=TRUE, this additional item has the CV info for each of the mixed fits. In particular it also selects lambda, gamma pairs corresponding to the 1SE rule, as well as the minimum error.

Details

The function runs glmnet nfolds+1 times; the first to get the lambda sequence, and then the remainder to compute the fit with each of the folds omitted. The error is accumulated, and the average error and standard deviation over the folds is computed. Note that cv.glmnet does NOT search for values for alpha. A specific value should be supplied, else alpha=1 is assumed by default. If users would like to cross-validate alpha as well, they should call cv.glmnet with a pre-computed vector foldid, and then use this same fold vector in separate calls to cv.glmnet with different values of alpha. Note also that the results of cv.glmnet are random, since the folds are selected at random. Users can reduce this randomness by running cv.glmnet many times, and averaging the error curves.

If relax=TRUE then the values of gamma are used to mix the fits. If \(\eta\) is the fit for lasso/elastic net, and \(\eta_R\) is the relaxed fit (with unpenalized coefficients), then a relaxed fit mixed by \(\gamma\) is $$\eta(\gamma)=(1-\gamma)\eta_R+\gamma\eta$$. There is practically no extra cost for having a lot of values for gamma. However, 5 seems sufficient for most purposes. CV then selects both gamma and lambda.

References

Friedman, J., Hastie, T. and Tibshirani, R. (2008) Regularization Paths for Generalized Linear Models via Coordinate Descent, https://web.stanford.edu/~hastie/Papers/glmnet.pdf
Journal of Statistical Software, Vol. 33(1), 1-22 Feb 2010
https://www.jstatsoft.org/v33/i01/
Simon, N., Friedman, J., Hastie, T., Tibshirani, R. (2011) Regularization Paths for Cox's Proportional Hazards Model via Coordinate Descent, Journal of Statistical Software, Vol. 39(5) 1-13
https://www.jstatsoft.org/v39/i05/

See also

glmnet and plot, predict, and coef methods for "cv.glmnet" and "cv.relaxed" objects.

Examples

set.seed(1010)
n = 1000
p = 100
nzc = trunc(p/10)
x = matrix(rnorm(n * p), n, p)
beta = rnorm(nzc)
fx = x[, seq(nzc)] %*% beta
eps = rnorm(n) * 5
y = drop(fx + eps)
px = exp(fx)
px = px/(1 + px)
ly = rbinom(n = length(px), prob = px, size = 1)
set.seed(1011)
cvob1 = cv.glmnet(x, y)
plot(cvob1)
coef(cvob1)
#> 101 x 1 sparse Matrix of class "dgCMatrix"
#>                      1
#> (Intercept) -0.1162737
#> V1          -0.2171531
#> V2           0.3237422
#> V3           .        
#> V4          -0.2190339
#> V5          -0.1856601
#> V6           0.2530652
#> V7           0.1874832
#> V8          -1.3574323
#> V9           1.0162046
#> V10          0.1558299
#> V11          .        
#> V12          .        
#> V13          .        
#> V14          .        
#> V15          .        
#> V16          .        
#> V17          .        
#> V18          .        
#> V19          .        
#> V20          .        
#> V21          .        
#> V22          .        
#> V23          .        
#> V24          .        
#> V25          .        
#> V26          .        
#> V27          .        
#> V28          .        
#> V29          .        
#> V30          .        
#> V31          .        
#> V32          .        
#> V33          .        
#> V34          .        
#> V35          .        
#> V36          .        
#> V37          .        
#> V38          .        
#> V39          .        
#> V40          .        
#> V41          .        
#> V42          .        
#> V43          .        
#> V44          .        
#> V45          .        
#> V46          .        
#> V47          .        
#> V48          .        
#> V49          .        
#> V50          .        
#> V51          .        
#> V52          .        
#> V53          .        
#> V54          .        
#> V55          .        
#> V56          .        
#> V57          .        
#> V58          .        
#> V59          .        
#> V60          .        
#> V61          .        
#> V62          .        
#> V63          .        
#> V64          .        
#> V65          .        
#> V66          .        
#> V67          .        
#> V68          .        
#> V69          .        
#> V70          .        
#> V71          .        
#> V72          .        
#> V73          .        
#> V74          .        
#> V75         -0.1420966
#> V76          .        
#> V77          .        
#> V78          .        
#> V79          .        
#> V80          .        
#> V81          .        
#> V82          .        
#> V83          .        
#> V84          .        
#> V85          .        
#> V86          .        
#> V87          .        
#> V88          .        
#> V89          .        
#> V90          .        
#> V91          .        
#> V92          .        
#> V93          .        
#> V94          .        
#> V95          .        
#> V96          .        
#> V97          .        
#> V98          .        
#> V99          .        
#> V100         .        
predict(cvob1, newx = x[1:5, ], s = "lambda.min")
#>               1
#> [1,] -1.3447658
#> [2,]  0.9443441
#> [3,]  0.6989746
#> [4,]  1.8698290
#> [5,] -4.7372693
title("Gaussian Family", line = 2.5)
set.seed(1011)
cvob1a = cv.glmnet(x, y, type.measure = "mae")
plot(cvob1a)
title("Gaussian Family", line = 2.5)
set.seed(1011)
par(mfrow = c(2, 2), mar = c(4.5, 4.5, 4, 1))
cvob2 = cv.glmnet(x, ly, family = "binomial")
plot(cvob2)
title("Binomial Family", line = 2.5)
frame()
set.seed(1011)
cvob3 = cv.glmnet(x, ly, family = "binomial", type.measure = "class")
plot(cvob3)
title("Binomial Family", line = 2.5)
if (FALSE) {
cvob1r = cv.glmnet(x, y, relax = TRUE)
plot(cvob1r)
predict(cvob1r, newx = x[, 1:5])
set.seed(1011)
cvob3a = cv.glmnet(x, ly, family = "binomial", type.measure = "auc")
plot(cvob3a)
title("Binomial Family", line = 2.5)
set.seed(1011)
mu = exp(fx/10)
y = rpois(n, mu)
cvob4 = cv.glmnet(x, y, family = "poisson")
plot(cvob4)
title("Poisson Family", line = 2.5)

# Multinomial
n = 500
p = 30
nzc = trunc(p/10)
x = matrix(rnorm(n * p), n, p)
beta3 = matrix(rnorm(30), 10, 3)
beta3 = rbind(beta3, matrix(0, p - 10, 3))
f3 = x %*% beta3
p3 = exp(f3)
p3 = p3/apply(p3, 1, sum)
g3 = glmnet:::rmult(p3)
set.seed(10101)
cvfit = cv.glmnet(x, g3, family = "multinomial")
plot(cvfit)
title("Multinomial Family", line = 2.5)
# Cox
beta = rnorm(nzc)
fx = x[, seq(nzc)] %*% beta/3
hx = exp(fx)
ty = rexp(n, hx)
tcens = rbinom(n = n, prob = 0.3, size = 1)  # censoring indicator
y = cbind(time = ty, status = 1 - tcens)  # y=Surv(ty,1-tcens) with library(survival)
foldid = sample(rep(seq(10), length = n))
fit1_cv = cv.glmnet(x, y, family = "cox", foldid = foldid)
plot(fit1_cv)
title("Cox Family", line = 2.5)
# Parallel
require(doMC)
registerDoMC(cores = 4)
x = matrix(rnorm(1e+05 * 100), 1e+05, 100)
y = rnorm(1e+05)
system.time(cv.glmnet(x, y))
system.time(cv.glmnet(x, y, parallel = TRUE))
}