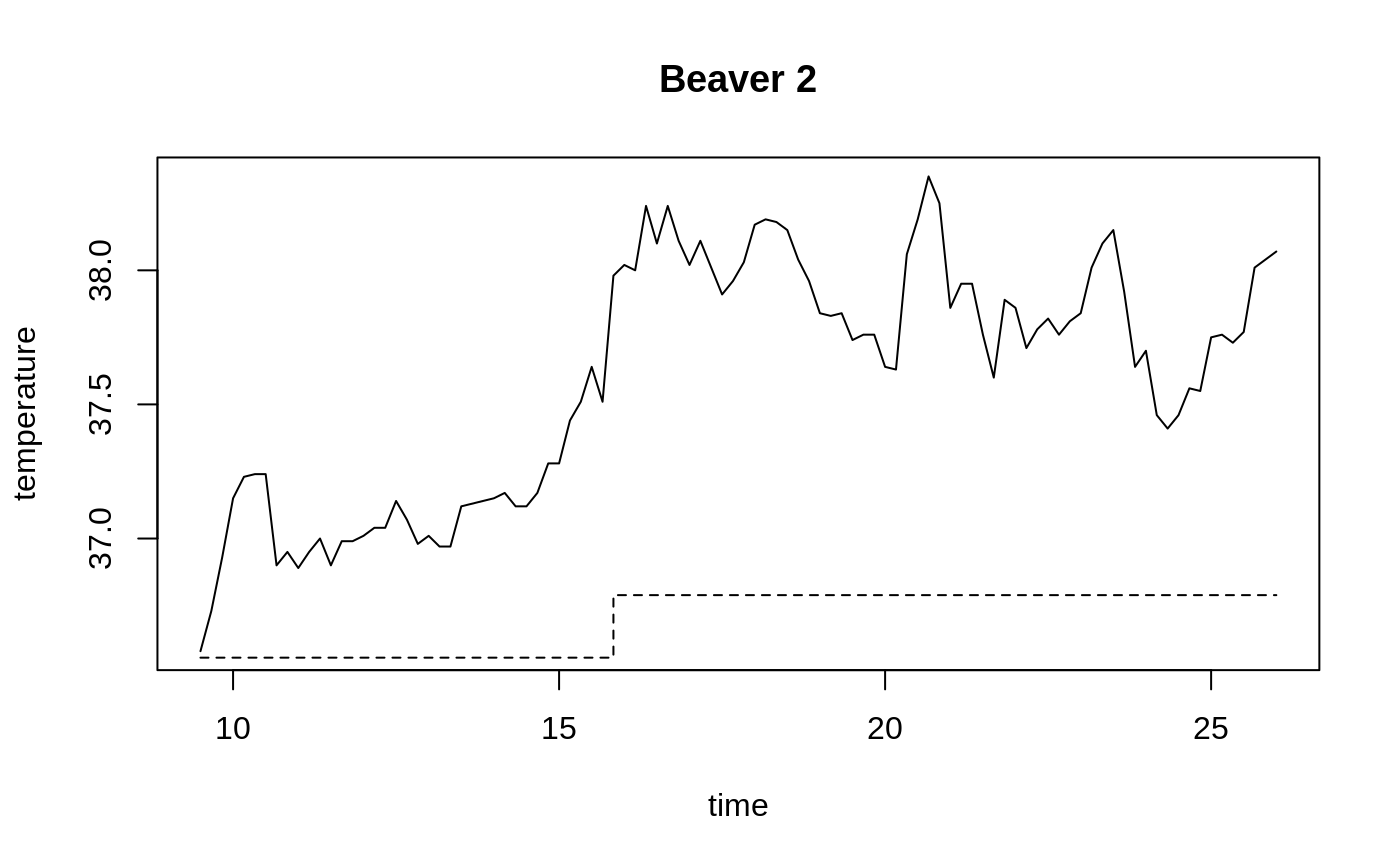
Body Temperature Series of Beaver 2

Reynolds (1994) describes a small part of a study of the long-term temperature dynamics of beaver Castor canadensis in north-central Wisconsin. Body temperature was measured by telemetry every 10 minutes for four females, but data from a one period of less than a day for each of two animals is used there.

beav2

Format

The beav2 data frame has 100 rows and 4 columns. This data frame contains the following columns:

day

Day of observation (in days since the beginning of 1990), November 3--4.

time

Time of observation, in the form 0330 for 3.30am.

temp

Measured body temperature in degrees Celsius.

activ

Indicator of activity outside the retreat.

Source

P. S. Reynolds (1994) Time-series analyses of beaver body temperatures. Chapter 11 of Lange, N., Ryan, L., Billard, L., Brillinger, D., Conquest, L. and Greenhouse, J. eds (1994) Case Studies in Biometry. New York: John Wiley and Sons.

References

Venables, W. N. and Ripley, B. D. (2002) Modern Applied Statistics with S. Fourth edition. Springer.

See also

beav1

Examples

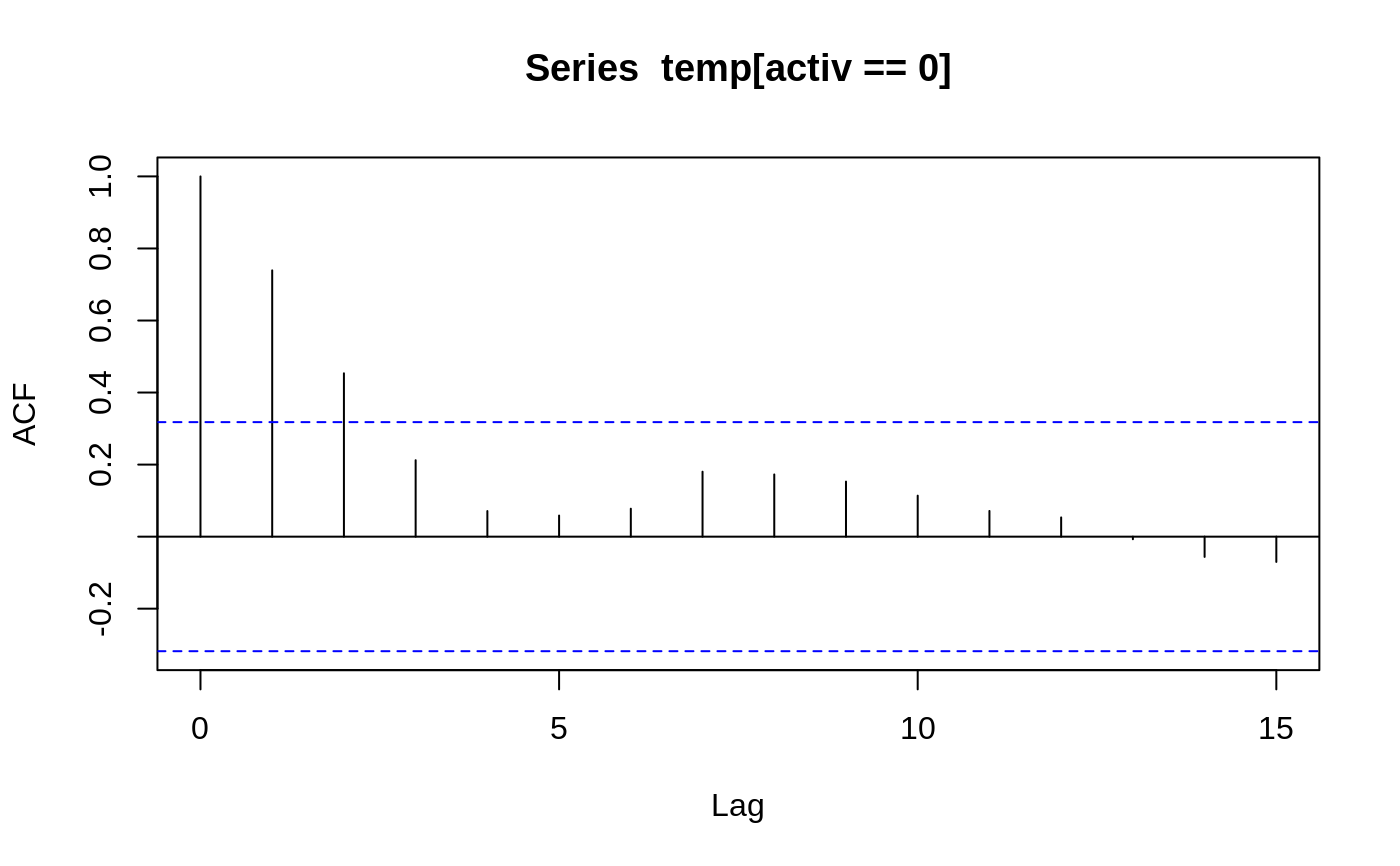
attach(beav2)
beav2$hours <- 24*(day-307) + trunc(time/100) + (time%%100)/60
plot(beav2$hours, beav2$temp, type = "l", xlab = "time",
   ylab = "temperature", main = "Beaver 2")
usr <- par("usr"); usr[3:4] <- c(-0.2, 8); par(usr = usr)
lines(beav2$hours, beav2$activ, type = "s", lty = 2)

temp <- ts(temp, start = 8+2/3, frequency = 6)
activ <- ts(activ, start = 8+2/3, frequency = 6)
acf(temp[activ == 0]); acf(temp[activ == 1]) # also look at PACFs
ar(temp[activ == 0]); ar(temp[activ == 1])
#> 
#> Call:
#> ar(x = temp[activ == 0])
#> 
#> Coefficients:
#>      1  
#> 0.7392  
#> 
#> Order selected 1  sigma^2 estimated as  0.02011
#> 
#> Call:
#> ar(x = temp[activ == 1])
#> 
#> Coefficients:
#>      1  
#> 0.7894  
#> 
#> Order selected 1  sigma^2 estimated as  0.01792

arima(temp, order = c(1,0,0), xreg = activ)
#> 
#> Call:
#> arima(x = temp, order = c(1, 0, 0), xreg = activ)
#> 
#> Coefficients:
#>          ar1  intercept   activ
#>       0.8733    37.1920  0.6139
#> s.e.  0.0684     0.1187  0.1381
#> 
#> sigma^2 estimated as 0.01518:  log likelihood = 66.78,  aic = -125.55
dreg <- cbind(sin = sin(2*pi*beav2$hours/24), cos = cos(2*pi*beav2$hours/24))
arima(temp, order = c(1,0,0), xreg = cbind(active=activ, dreg))
#> 
#> Call:
#> arima(x = temp, order = c(1, 0, 0), xreg = cbind(active = activ, dreg))
#> 
#> Coefficients:
#>          ar1  intercept  active  dreg.sin  dreg.cos
#>       0.7905    37.1674  0.5322    -0.282    0.1201
#> s.e.  0.0681     0.0939  0.1282     0.105    0.0997
#> 
#> sigma^2 estimated as 0.01434:  log likelihood = 69.83,  aic = -127.67

library(nlme) # for gls and corAR1
beav2.gls <- gls(temp ~ activ, data = beav2, corr = corAR1(0.8),
                 method = "ML")
summary(beav2.gls)
#> Generalized least squares fit by maximum likelihood
#>   Model: temp ~ activ 
#>   Data: beav2 
#>         AIC       BIC   logLik
#>   -125.5505 -115.1298 66.77523
#> 
#> Correlation Structure: AR(1)
#>  Formula: ~1 
#>  Parameter estimate(s):
#>       Phi 
#> 0.8731771 
#> 
#> Coefficients:
#>                Value Std.Error  t-value p-value
#> (Intercept) 37.19195 0.1131328 328.7460       0
#> activ        0.61418 0.1087286   5.6487       0
#> 
#>  Correlation: 
#>       (Intr)
#> activ -0.582
#> 
#> Standardized residuals:
#>         Min          Q1         Med          Q3         Max 
#> -2.42080780 -0.61510520 -0.03573836  0.81641138  2.15153499 
#> 
#> Residual standard error: 0.2527856 
#> Degrees of freedom: 100 total; 98 residual
summary(update(beav2.gls, subset = 6:100))
#> Generalized least squares fit by maximum likelihood
#>   Model: temp ~ activ 
#>   Data: beav2 
#>   Subset: 6:100 
#>        AIC       BIC   logLik
#>   -124.981 -114.7654 66.49048
#> 
#> Correlation Structure: AR(1)
#>  Formula: ~1 
#>  Parameter estimate(s):
#>       Phi 
#> 0.8380448 
#> 
#> Coefficients:
#>                Value  Std.Error  t-value p-value
#> (Intercept) 37.25001 0.09634047 386.6496       0
#> activ        0.60277 0.09931904   6.0690       0
#> 
#>  Correlation: 
#>       (Intr)
#> activ -0.657
#> 
#> Standardized residuals:
#>        Min         Q1        Med         Q3        Max 
#> -2.0231494 -0.8910348 -0.1497564  0.7640939  2.2719468 
#> 
#> Residual standard error: 0.2188542 
#> Degrees of freedom: 95 total; 93 residual
detach("beav2"); rm(temp, activ)