Gap Statistic for Estimating the Number of Clusters

clusGap() calculates a goodness of clustering measure, the “gap” statistic. For each number of clusters $k$, it compares $\log(W(k))$ with $E^*[\log(W(k))]$ where the latter is defined via bootstrapping, i.e., simulating from a reference ($H_0$) distribution, a uniform distribution on the hypercube determined by the ranges of x, after first centering, and then svd (aka ‘PCA’)-rotating them when (as by default) spaceH0 = "scaledPCA".

maxSE(f, SE.f) determines the location of the maximum of f, taking a “1-SE rule” into account for the *SE* methods. The default method "firstSEmax" looks for the smallest $k$ such that its value $f(k)$ is not more than 1 standard error away from the first local maximum. This is similar but not the same as "Tibs2001SEmax", Tibshirani et al's recommendation of determining the number of clusters from the gap statistics and their standard deviations.

clusGap(x, FUNcluster, K.max, B = 100, d.power = 1,
        spaceH0 = c("scaledPCA", "original"),
        verbose = interactive(), ...)

maxSE(f, SE.f,
      method = c("firstSEmax", "Tibs2001SEmax", "globalSEmax",
                 "firstmax", "globalmax"),
      SE.factor = 1)

# S3 method for clusGap
print(x, method = "firstSEmax", SE.factor = 1, ...)

# S3 method for clusGap
plot(x, type = "b", xlab = "k", ylab = expression(Gap[k]),
     main = NULL, do.arrows = TRUE,
     arrowArgs = list(col="red3", length=1/16, angle=90, code=3), ...)

Arguments

x	numeric matrix or `data.frame`.
FUNcluster	a `function` which accepts as first argument a (data) matrix like `x`, second argument, say $k, k\geq 2$, the number of clusters desired, and returns a `list` with a component named (or shortened to) `cluster` which is a vector of length `n = nrow(x)` of integers in `1:k` determining the clustering or grouping of the `n` observations.
K.max	the maximum number of clusters to consider, must be at least two.
B	integer, number of Monte Carlo (“bootstrap”) samples.
d.power	a positive integer specifying the power $p$ which is applied to the euclidean distances (`dist`) before they are summed up to give $W(k)$. The default, `d.power = 1`, corresponds to the “historical” R implementation, whereas `d.power = 2` corresponds to what Tibshirani et al had proposed. This was found by Juan Gonzalez, in 2016-02.
spaceH0	a `character` string specifying the space of the $H_0$ distribution (of no cluster). Both `"scaledPCA"` and `"original"` use a uniform distribution in a hyper cube and had been mentioned in the reference; `"original"` been added after a proposal (including code) by Juan Gonzalez.
verbose	integer or logical, determining if “progress” output should be printed. The default prints one bit per bootstrap sample.
...	(for `clusGap()`:) optionally further arguments for `FUNcluster()`, see `kmeans` example below.
f	numeric vector of ‘function values’, of length $K$, whose (“1 SE respected”) maximum we want.
SE.f	numeric vector of length $K$ of standard errors of `f`.
method	character string indicating how the “optimal” number of clusters, $\hat k$, is computed from the gap statistics (and their standard deviations), or more generally how the location $\hat k$ of the maximum of $f_k$ should be determined. `"globalmax"`: simply corresponds to the global maximum, i.e., is `which.max(f)` `"firstmax"`: gives the location of the first local maximum. `"Tibs2001SEmax"`: uses the criterion, Tibshirani et al (2001) proposed: “the smallest $k$ such that $f(k) \ge f(k+1) - s_{k+1}$”. Note that this chooses $k = 1$ when all standard deviations are larger than the differences $f(k+1) - f(k)$. `"firstSEmax"`: location of the first $f()$ value which is not smaller than the first local maximum minus `SE.factor * SE.f[]`, i.e, within an “f S.E.” range of that maximum (see also `SE.factor`). This, the default, has been proposed by Martin Maechler in 2012, when adding `clusGap()` to the cluster package, after having seen the `"globalSEmax"` proposal (in code) and read the `"Tibs2001SEmax"` proposal. `"globalSEmax"`: (used in Dudoit and Fridlyand (2002), supposedly following Tibshirani's proposition): location of the first $f()$ value which is not smaller than the global maximum minus `SE.factor * SE.f[]`, i.e, within an “f S.E.” range of that maximum (see also `SE.factor`). See the examples for a comparison in a simple case.
SE.factor	[When `method` contains `"SE"`] Determining the optimal number of clusters, Tibshirani et al. proposed the “1 S.E.”-rule. Using an `SE.factor` $f$, the “f S.E.”-rule is used, more generally.
type, xlab, ylab, main	arguments with the same meaning as in `plot.default()`, with different default.
do.arrows	logical indicating if (1 SE -)“error bars” should be drawn, via `arrows()`.
arrowArgs	a list of arguments passed to `arrows()`; the default, notably `angle` and `code`, provide a style matching usual error bars.

Details

The main result <res>$Tab[,"gap"] of course is from bootstrapping aka Monte Carlo simulation and hence random, or equivalently, depending on the initial random seed (see set.seed()). On the other hand, in our experience, using B = 500 gives quite precise results such that the gap plot is basically unchanged after an another run.

Value

clusGap(..) returns an object of S3 class "clusGap", basically a list with components

Tab

a matrix with K.max rows and 4 columns, named "logW", "E.logW", "gap", and "SE.sim", where gap = E.logW - logW, and SE.sim corresponds to the standard error of gap, SE.sim[k]=$s_k$, where $s_k := \sqrt{1 + 1/B} sd^*(gap_j)$, and $sd^*()$ is the standard deviation of the simulated (“bootstrapped”) gap values.

call

the clusGap(..) call.

spaceH0

the spaceH0 argument (match.arg()ed).

number of observations, i.e., nrow(x).

input B

FUNcluster

input function FUNcluster

References

Tibshirani, R., Walther, G. and Hastie, T. (2001). Estimating the number of data clusters via the Gap statistic. Journal of the Royal Statistical Society B, 63, 411--423.

Tibshirani, R., Walther, G. and Hastie, T. (2000). Estimating the number of clusters in a dataset via the Gap statistic. Technical Report. Stanford.

Dudoit, S. and Fridlyand, J. (2002) A prediction-based resampling method for estimating the number of clusters in a dataset. Genome Biology 3(7). doi: 10.1186/gb-2002-3-7-research0036

Per Broberg (2006). SAGx: Statistical Analysis of the GeneChip. R package version 1.9.7. http://www.bioconductor.org/packages/release/bioc/html/SAGx.html

Examples

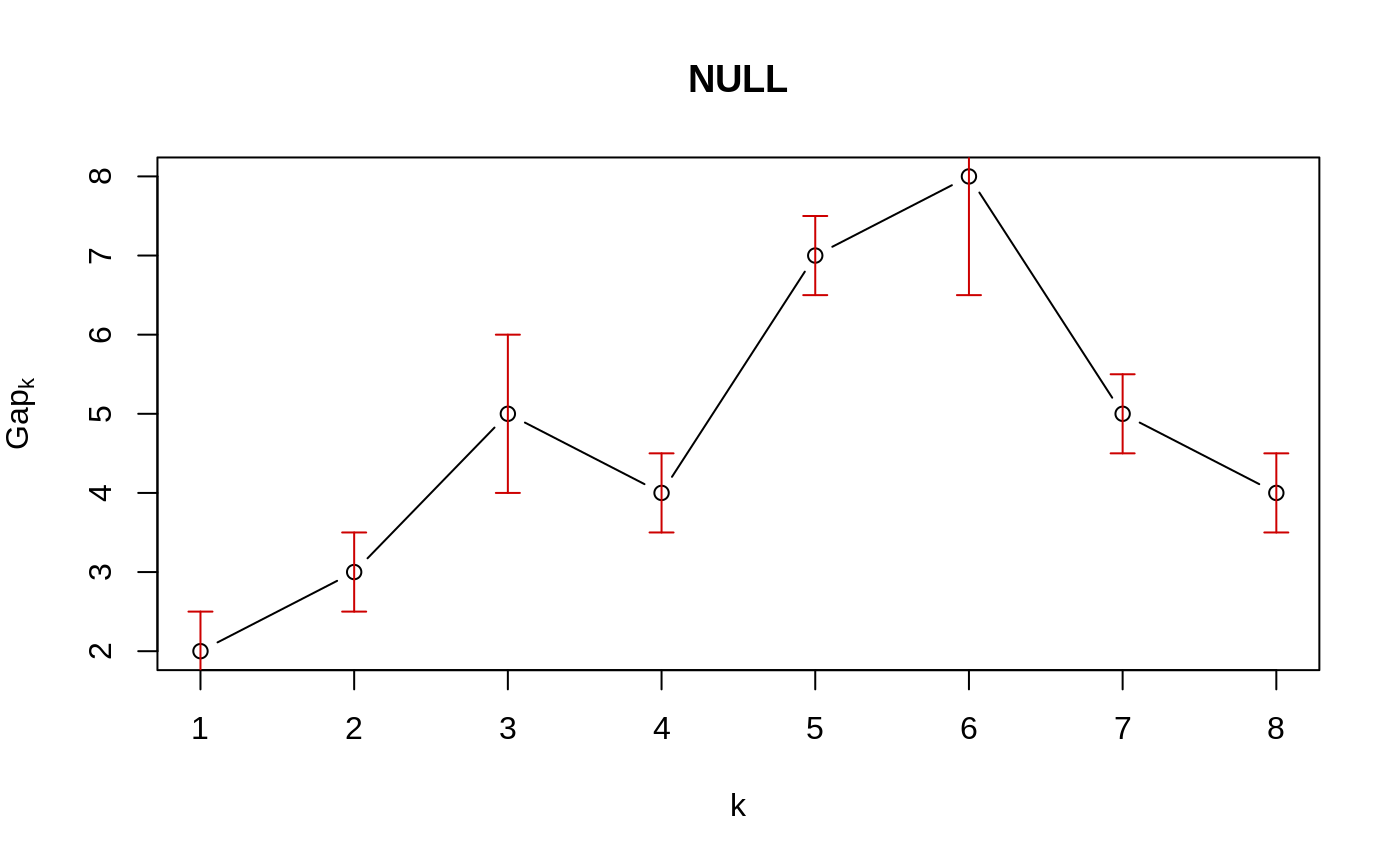
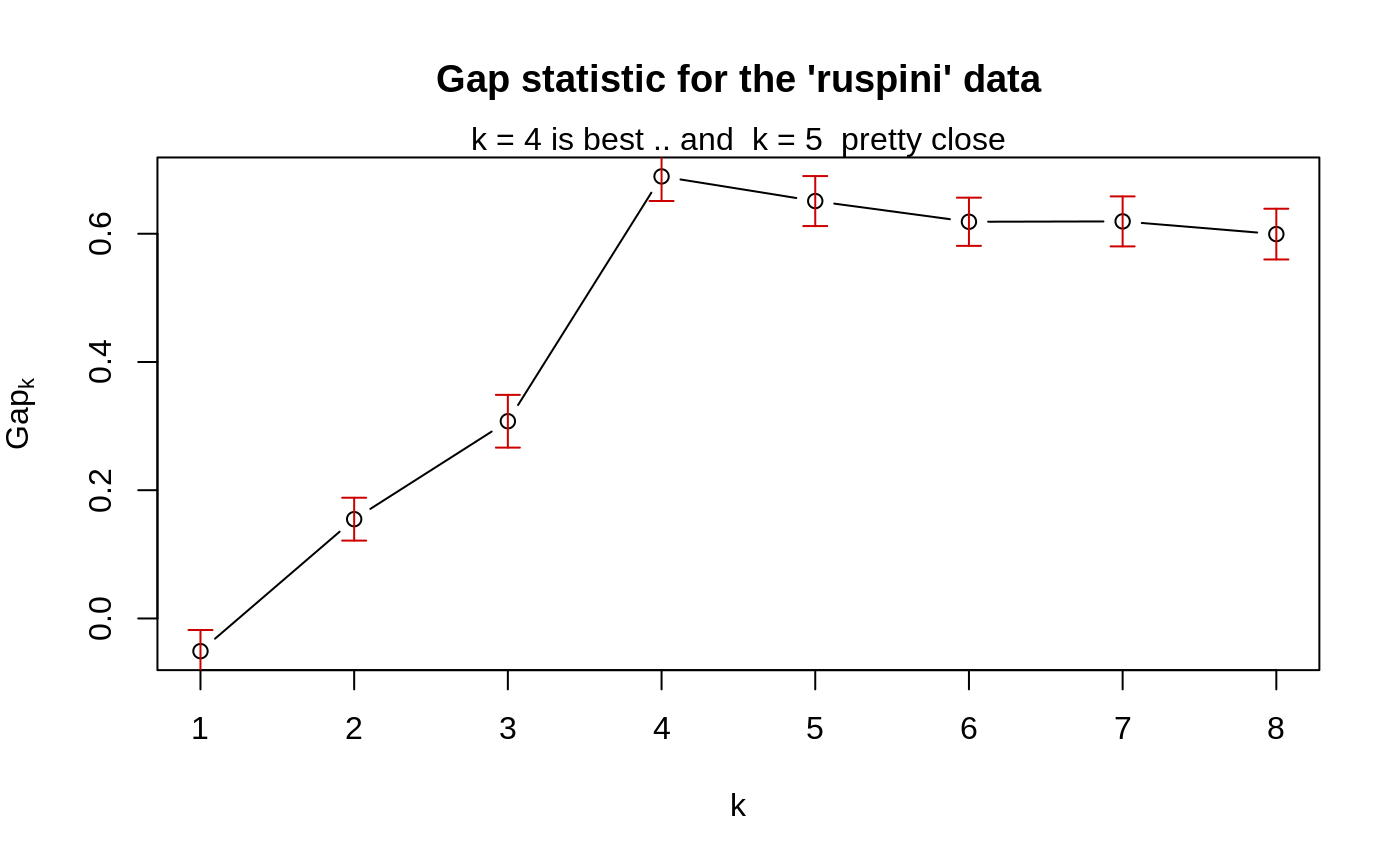
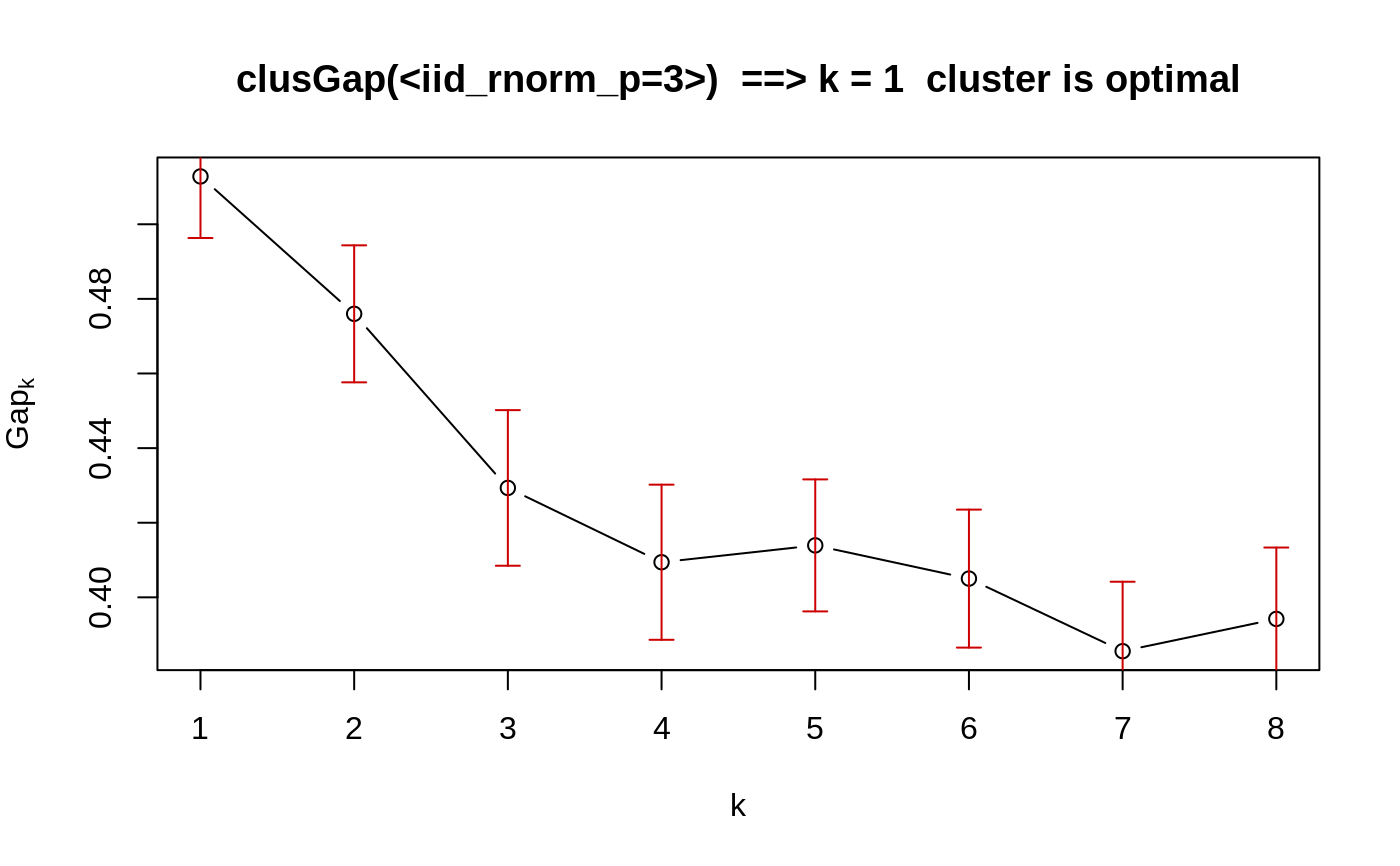
### --- maxSE() methods -------------------------------------------
(mets <- eval(formals(maxSE)$method))
#> [1] "firstSEmax"    "Tibs2001SEmax" "globalSEmax"   "firstmax"     
#> [5] "globalmax"    
fk <- c(2,3,5,4,7,8,5,4)
sk <- c(1,1,2,1,1,3,1,1)/2
## use plot.clusGap():
plot(structure(class="clusGap", list(Tab = cbind(gap=fk, SE.sim=sk))))
## Note that 'firstmax' and 'globalmax' are always at 3 and 6 :
sapply(c(1/4, 1,2,4), function(SEf)
        sapply(mets, function(M) maxSE(fk, sk, method = M, SE.factor = SEf)))
#>               [,1] [,2] [,3] [,4]
#> firstSEmax       3    3    2    1
#> Tibs2001SEmax    3    3    1    1
#> globalSEmax      6    5    3    1
#> firstmax         3    3    3    3
#> globalmax        6    6    6    6

### --- clusGap() -------------------------------------------------
## ridiculously nicely separated clusters in 3 D :
x <- rbind(matrix(rnorm(150,           sd = 0.1), ncol = 3),
           matrix(rnorm(150, mean = 1, sd = 0.1), ncol = 3),
           matrix(rnorm(150, mean = 2, sd = 0.1), ncol = 3),
           matrix(rnorm(150, mean = 3, sd = 0.1), ncol = 3))

## Slightly faster way to use pam (see below)
pam1 <- function(x,k) list(cluster = pam(x,k, cluster.only=TRUE))

## We do not recommend using hier.clustering here, but if you want,
## there is  factoextra::hcut () or a cheap version of it
hclusCut <- function(x, k, d.meth = "euclidean", ...)
   list(cluster = cutree(hclust(dist(x, method=d.meth), ...), k=k))

## You can manually set it before running this :    doExtras <- TRUE  # or  FALSE
if(!(exists("doExtras") && is.logical(doExtras)))
  doExtras <- cluster:::doExtras()

if(doExtras) {
  ## Note we use  B = 60 in the following examples to keep them "speedy".
  ## ---- rather keep the default B = 500 for your analysis!

  ## note we can  pass 'nstart = 20' to kmeans() :
  gskmn <- clusGap(x, FUN = kmeans, nstart = 20, K.max = 8, B = 60)
  gskmn #-> its print() method
  plot(gskmn, main = "clusGap(., FUN = kmeans, n.start=20, B= 60)")
  set.seed(12); system.time(
    gsPam0 <- clusGap(x, FUN = pam, K.max = 8, B = 60)
  )
  set.seed(12); system.time(
    gsPam1 <- clusGap(x, FUN = pam1, K.max = 8, B = 60)
  )
  ## and show that it gives the "same":
  not.eq <- c("call", "FUNcluster"); n <- names(gsPam0)
  eq <- n[!(n %in% not.eq)]
  stopifnot(identical(gsPam1[eq], gsPam0[eq]))
  print(gsPam1, method="globalSEmax")
  print(gsPam1, method="globalmax")

  print(gsHc <- clusGap(x, FUN = hclusCut, K.max = 8, B = 60))

}# end {doExtras}

gs.pam.RU <- clusGap(ruspini, FUN = pam1, K.max = 8, B = 60)
gs.pam.RU
#> Clustering Gap statistic ["clusGap"] from call:
#> clusGap(x = ruspini, FUNcluster = pam1, K.max = 8, B = 60)
#> B=60 simulated reference sets, k = 1..8; spaceH0="scaledPCA"
#>  --> Number of clusters (method 'firstSEmax', SE.factor=1): 4
#>          logW   E.logW         gap     SE.sim
#> [1,] 7.187997 7.136986 -0.05101103 0.03302558
#> [2,] 6.628498 6.783334  0.15483620 0.03342620
#> [3,] 6.261660 6.569243  0.30758376 0.04110513
#> [4,] 5.692736 6.382139  0.68940274 0.03830180
#> [5,] 5.580999 6.231987  0.65098780 0.03900937
#> [6,] 5.500583 6.119283  0.61869983 0.03754351
#> [7,] 5.394195 6.013466  0.61927144 0.03895899
#> [8,] 5.320052 5.919497  0.59944507 0.03956904
plot(gs.pam.RU, main = "Gap statistic for the 'ruspini' data")
mtext("k = 4 is best .. and  k = 5  pretty close")

## This takes a minute..
## No clustering ==> k = 1 ("one cluster") should be optimal:
Z <- matrix(rnorm(256*3), 256,3)
gsP.Z <- clusGap(Z, FUN = pam1, K.max = 8, B = 200)
plot(gsP.Z, main = "clusGap(<iid_rnorm_p=3>)  ==> k = 1  cluster is optimal")
gsP.Z
#> Clustering Gap statistic ["clusGap"] from call:
#> clusGap(x = Z, FUNcluster = pam1, K.max = 8, B = 200)
#> B=200 simulated reference sets, k = 1..8; spaceH0="scaledPCA"
#>  --> Number of clusters (method 'firstSEmax', SE.factor=1): 1
#>          logW   E.logW       gap     SE.sim
#> [1,] 4.929175 5.441996 0.5128202 0.01651083
#> [2,] 4.781765 5.257759 0.4759939 0.01836688
#> [3,] 4.682839 5.112167 0.4293272 0.02086095
#> [4,] 4.596303 5.005715 0.4094124 0.02078972
#> [5,] 4.501172 4.915102 0.4139299 0.01768952
#> [6,] 4.432367 4.837395 0.4050278 0.01849280
#> [7,] 4.386125 4.771698 0.3855738 0.01860643
#> [8,] 4.321455 4.715671 0.3942156 0.01913339

Author

This function is originally based on the functions gap of (Bioconductor) package SAGx by Per Broberg, gapStat() from former package SLmisc by Matthias Kohl and ideas from gap() and its methods of package lga by Justin Harrington.

The current implementation is by Martin Maechler.

The implementation of spaceH0 = "original" is based on code proposed by Juan Gonzalez.