Support Vector Machines

svm is used to train a support vector machine. It can be used to carry out general regression and classification (of nu and epsilon-type), as well as density-estimation. A formula interface is provided.

# S3 method for formula
svm(formula, data = NULL, ..., subset, na.action =
na.omit, scale = TRUE)
# S3 method for default
svm(x, y = NULL, scale = TRUE, type = NULL, kernel =
"radial", degree = 3, gamma = if (is.vector(x)) 1 else 1 / ncol(x),
coef0 = 0, cost = 1, nu = 0.5,
class.weights = NULL, cachesize = 40, tolerance = 0.001, epsilon = 0.1,
shrinking = TRUE, cross = 0, probability = FALSE, fitted = TRUE,
..., subset, na.action = na.omit)

Arguments

formula

a symbolic description of the model to be fit.
data

an optional data frame containing the variables in the model. By default the variables are taken from the environment which ‘svm’ is called from.
x

a data matrix, a vector, or a sparse matrix (object of class Matrix provided by the Matrix package, or of class matrix.csr provided by the SparseM package, or of class simple_triplet_matrix provided by the slam package).
y

a response vector with one label for each row/component of x. Can be either a factor (for classification tasks) or a numeric vector (for regression).
scale

A logical vector indicating the variables to be scaled. If scale is of length 1, the value is recycled as many times as needed. Per default, data are scaled internally (both x and y variables) to zero mean and unit variance. The center and scale values are returned and used for later predictions.
type

svm can be used as a classification machine, as a regression machine, or for novelty detection. Depending of whether y is a factor or not, the default setting for type is C-classification or eps-regression, respectively, but may be overwritten by setting an explicit value.
Valid options are:

  • C-classification

  • nu-classification

  • one-classification (for novelty detection)

  • eps-regression

  • nu-regression
kernel

the kernel used in training and predicting. You might consider changing some of the following parameters, depending on the kernel type.

linear:

\(u'v\)

polynomial:

\((\gamma u'v + coef0)^{degree}\)

radial basis:

\(e^(-\gamma |u-v|^2)\)

sigmoid:

\(tanh(\gamma u'v + coef0)\)
degree

parameter needed for kernel of type polynomial (default: 3)
gamma

parameter needed for all kernels except linear (default: 1/(data dimension))
coef0

parameter needed for kernels of type polynomial and sigmoid (default: 0)
cost

cost of constraints violation (default: 1)---it is the ‘C’-constant of the regularization term in the Lagrange formulation.
nu

parameter needed for nu-classification, nu-regression, and one-classification
class.weights

a named vector of weights for the different classes, used for asymmetric class sizes. Not all factor levels have to be supplied (default weight: 1). All components have to be named. Specifying "inverse" will choose the weights inversely proportional to the class distribution.
cachesize

cache memory in MB (default 40)
tolerance

tolerance of termination criterion (default: 0.001)
epsilon

epsilon in the insensitive-loss function (default: 0.1)
shrinking

option whether to use the shrinking-heuristics (default: TRUE)
cross

if a integer value k>0 is specified, a k-fold cross validation on the training data is performed to assess the quality of the model: the accuracy rate for classification and the Mean Squared Error for regression
fitted

logical indicating whether the fitted values should be computed and included in the model or not (default: TRUE)
probability

logical indicating whether the model should allow for probability predictions.
...

additional parameters for the low level fitting function svm.default
subset

An index vector specifying the cases to be used in the training sample. (NOTE: If given, this argument must be named.)
na.action

A function to specify the action to be taken if NAs are found. The default action is na.omit, which leads to rejection of cases with missing values on any required variable. An alternative is na.fail, which causes an error if NA cases are found. (NOTE: If given, this argument must be named.)

Value

An object of class "svm" containing the fitted model, including:

SV

The resulting support vectors (possibly scaled).

index

The index of the resulting support vectors in the data matrix. Note that this index refers to the preprocessed data (after the possible effect of na.omit and subset)

coefs

The corresponding coefficients times the training labels.

rho

The negative intercept.

sigma

In case of a probabilistic regression model, the scale parameter of the hypothesized (zero-mean) laplace distribution estimated by maximum likelihood.

probA, probB

numeric vectors of length k(k-1)/2, k number of classes, containing the parameters of the logistic distributions fitted to the decision values of the binary classifiers (1 / (1 + exp(a x + b))).

Details

For multiclass-classification with k levels, k>2, libsvm uses the ‘one-against-one’-approach, in which k(k-1)/2 binary classifiers are trained; the appropriate class is found by a voting scheme.

libsvm internally uses a sparse data representation, which is also high-level supported by the package SparseM.

If the predictor variables include factors, the formula interface must be used to get a correct model matrix.

plot.svm allows a simple graphical visualization of classification models.

The probability model for classification fits a logistic distribution using maximum likelihood to the decision values of all binary classifiers, and computes the a-posteriori class probabilities for the multi-class problem using quadratic optimization. The probabilistic regression model assumes (zero-mean) laplace-distributed errors for the predictions, and estimates the scale parameter using maximum likelihood.

For linear kernel, the coefficients of the regression/decision hyperplane can be extracted using the coef method (see examples).

Note

Data are scaled internally, usually yielding better results.

Parameters of SVM-models usually must be tuned to yield sensible results!

References

See also

predict.svm plot.svm tune.svm matrix.csr (in package SparseM)

Examples

data(iris)
attach(iris)
#> The following objects are masked from iris (pos = 4):
#> 
#>     Petal.Length, Petal.Width, Sepal.Length, Sepal.Width, Species

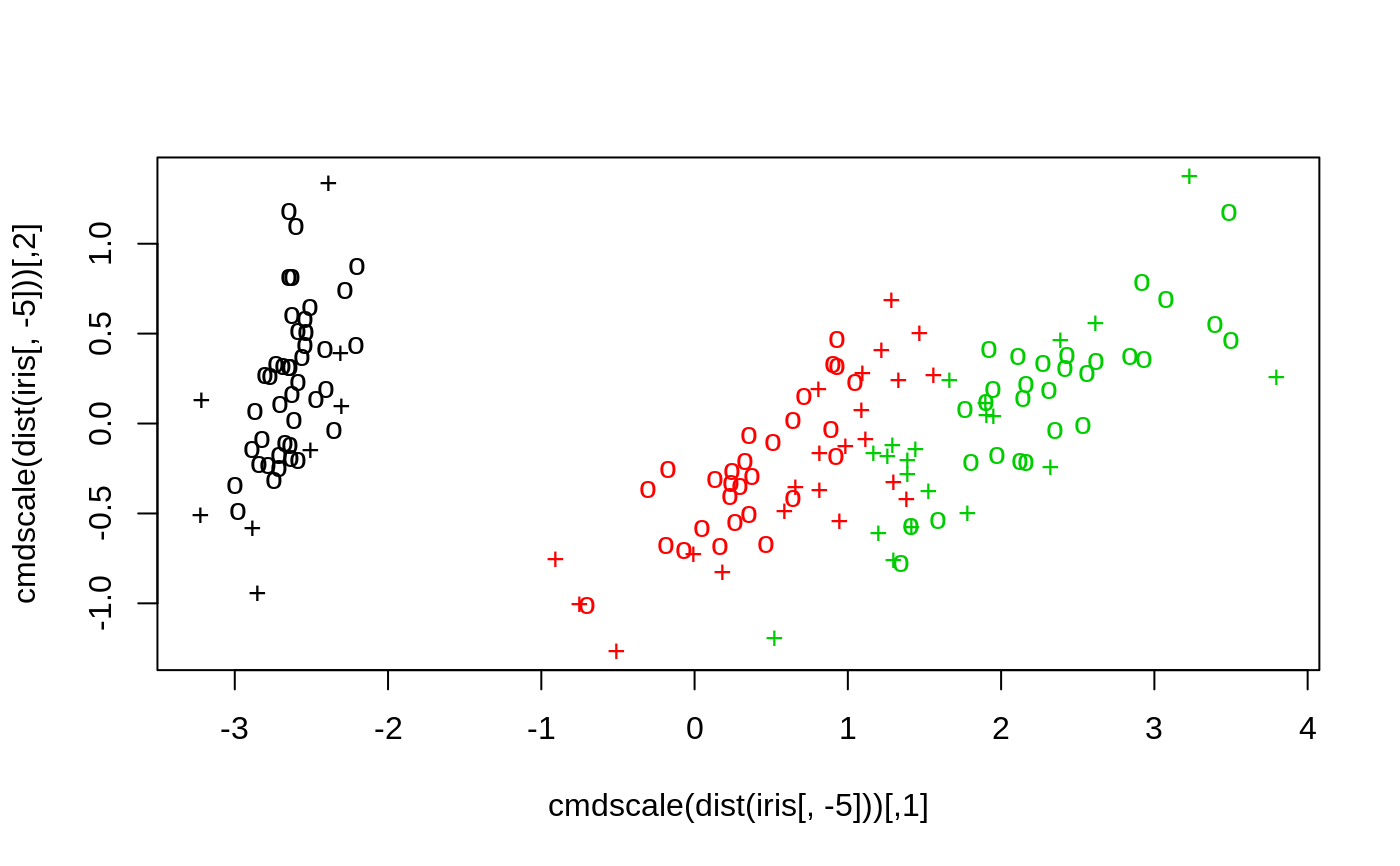
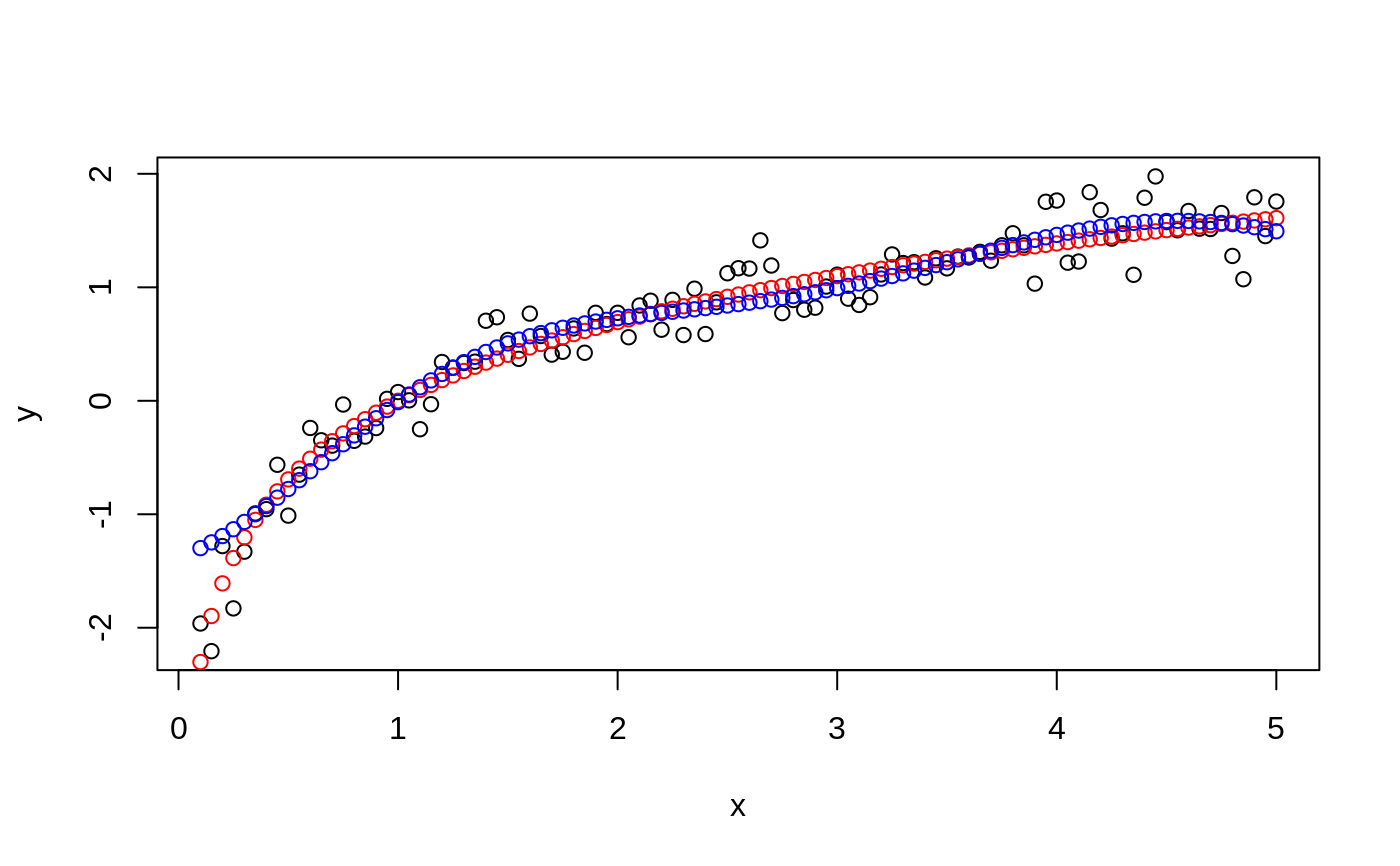
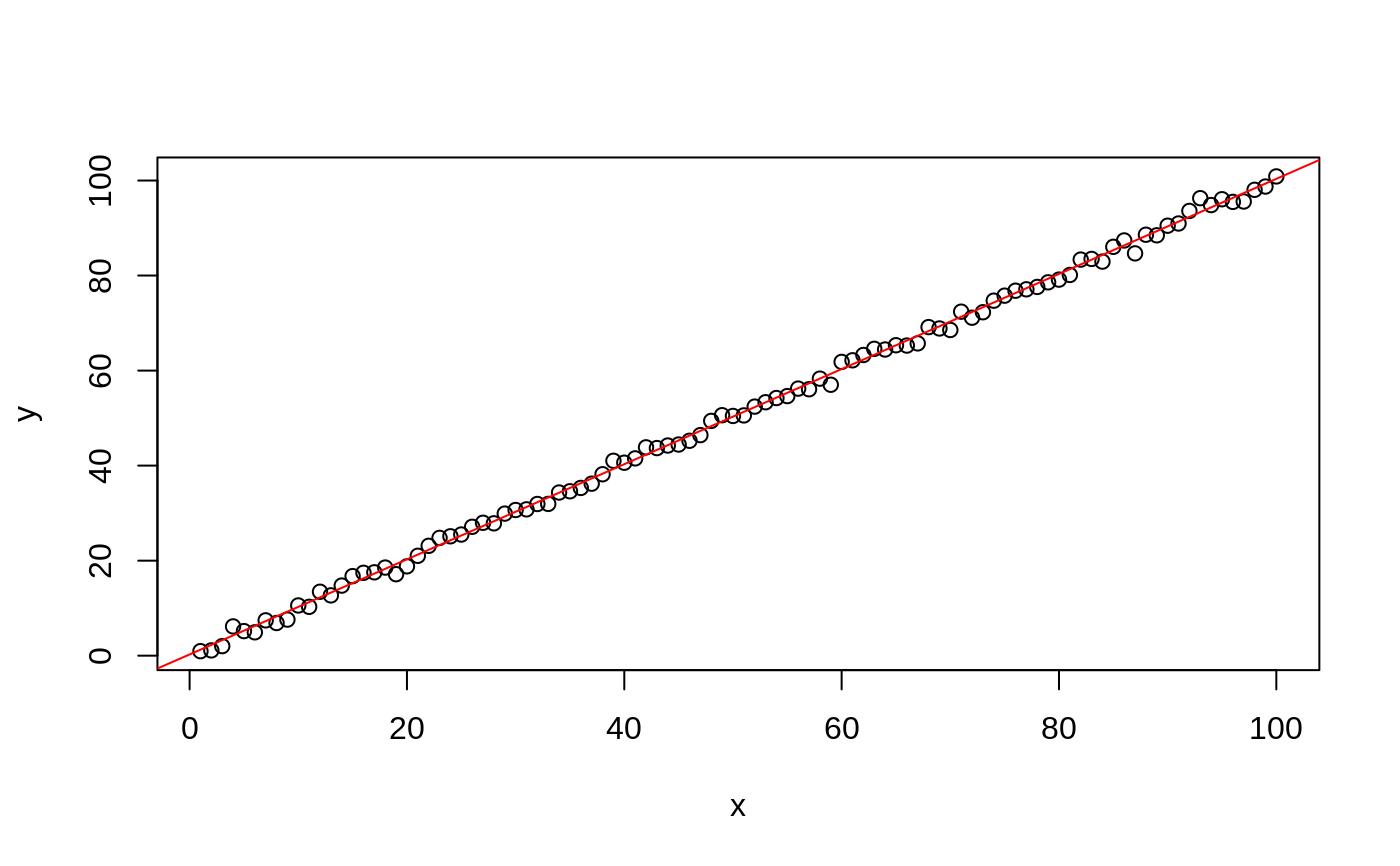
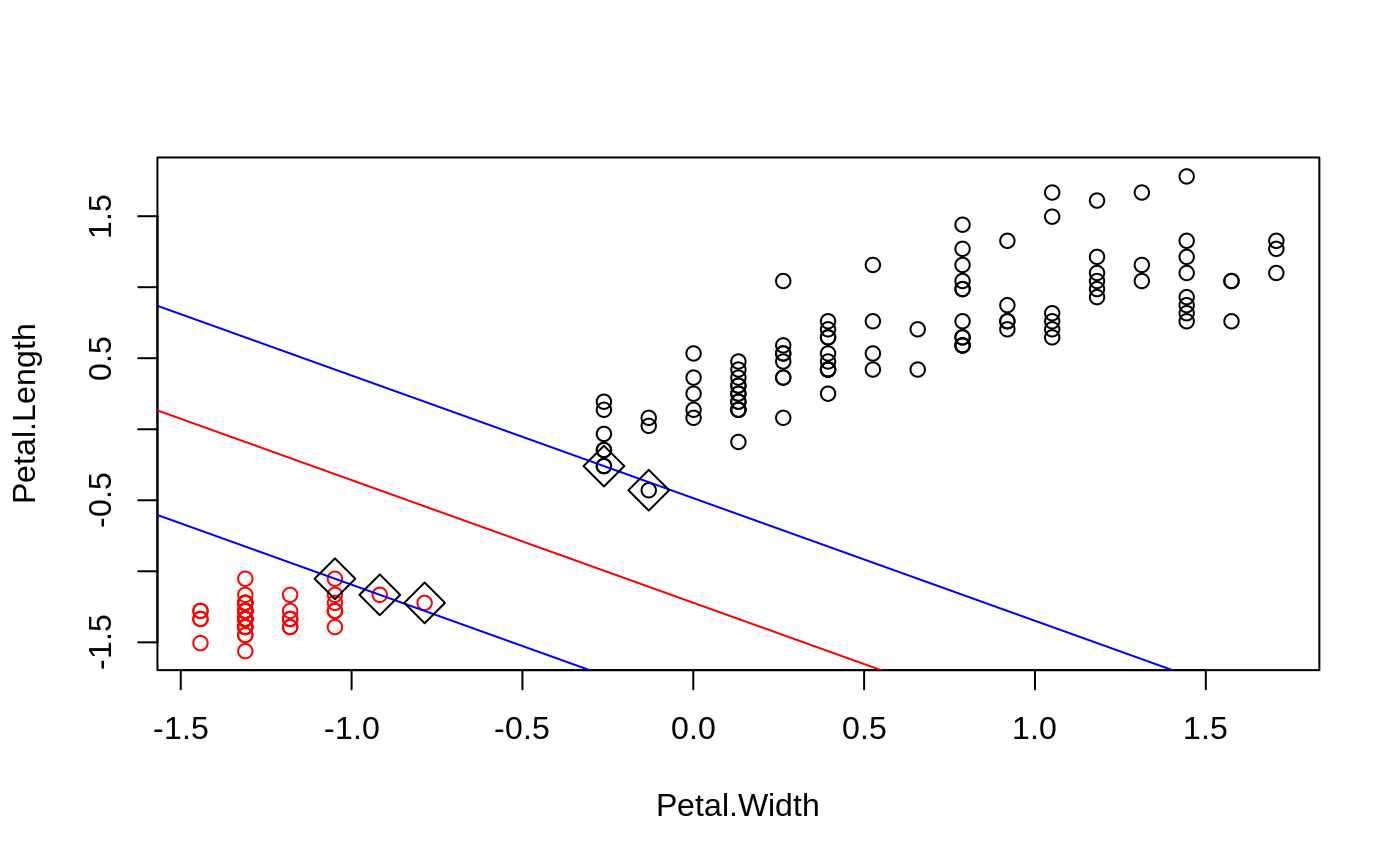
## classification mode
# default with factor response:
model <- svm(Species ~ ., data = iris)

# alternatively the traditional interface:
x <- subset(iris, select = -Species)
y <- Species
model <- svm(x, y)

print(model)
#> 
#> Call:
#> svm.default(x = x, y = y)
#> 
#> 
#> Parameters:
#>    SVM-Type:  C-classification 
#>  SVM-Kernel:  radial 
#>        cost:  1 
#> 
#> Number of Support Vectors:  51
#> 
summary(model)
#> 
#> Call:
#> svm.default(x = x, y = y)
#> 
#> 
#> Parameters:
#>    SVM-Type:  C-classification 
#>  SVM-Kernel:  radial 
#>        cost:  1 
#> 
#> Number of Support Vectors:  51
#> 
#>  ( 8 22 21 )
#> 
#> 
#> Number of Classes:  3 
#> 
#> Levels: 
#>  setosa versicolor virginica
#> 
#> 
#> 

# test with train data
pred <- predict(model, x)
# (same as:)
pred <- fitted(model)

# Check accuracy:
table(pred, y)
#>             y
#> pred         setosa versicolor virginica
#>   setosa         50          0         0
#>   versicolor      0         48         2
#>   virginica       0          2        48

# compute decision values and probabilities:
pred <- predict(model, x, decision.values = TRUE)
attr(pred, "decision.values")[1:4,]
#>   setosa/versicolor setosa/virginica versicolor/virginica
#> 1          1.196152         1.091757            0.6708810
#> 2          1.064621         1.056185            0.8483518
#> 3          1.180842         1.074542            0.6439798
#> 4          1.110699         1.053012            0.6782041

# visualize (classes by color, SV by crosses):
plot(cmdscale(dist(iris[,-5])),
     col = as.integer(iris[,5]),
     pch = c("o","+")[1:150 %in% model$index + 1])

## try regression mode on two dimensions

# create data
x <- seq(0.1, 5, by = 0.05)
y <- log(x) + rnorm(x, sd = 0.2)

# estimate model and predict input values
m   <- svm(x, y)
new <- predict(m, x)

# visualize
plot(x, y)
points(x, log(x), col = 2)
points(x, new, col = 4)

## density-estimation

# create 2-dim. normal with rho=0:
X <- data.frame(a = rnorm(1000), b = rnorm(1000))
attach(X)
#> The following objects are masked from X (pos = 4):
#> 
#>     a, b

# traditional way:
m <- svm(X, gamma = 0.1)

# formula interface:
m <- svm(~., data = X, gamma = 0.1)
# or:
m <- svm(~ a + b, gamma = 0.1)

# test:
newdata <- data.frame(a = c(0, 4), b = c(0, 4))
predict (m, newdata)
#>     1     2 
#>  TRUE FALSE 

# visualize:
plot(X, col = 1:1000 %in% m$index + 1, xlim = c(-5,5), ylim=c(-5,5))
points(newdata, pch = "+", col = 2, cex = 5)

## weights: (example not particularly sensible)
i2 <- iris
levels(i2$Species)[3] <- "versicolor"
summary(i2$Species)
#>     setosa versicolor 
#>         50        100 
wts <- 100 / table(i2$Species)
wts
#> 
#>     setosa versicolor 
#>          2          1 
m <- svm(Species ~ ., data = i2, class.weights = wts)

## extract coefficients for linear kernel

# a. regression
x <- 1:100
y <- x + rnorm(100)
m <- svm(y ~ x, scale = FALSE, kernel = "linear")
coef(m)
#> (Intercept)           x 
#>   0.2708256   1.0008886 
plot(y ~ x)
abline(m, col = "red")

# b. classification
# transform iris data to binary problem, and scale data
setosa <- as.factor(iris$Species == "setosa")
iris2 = scale(iris[,-5])

# fit binary C-classification model
m <- svm(setosa ~ Petal.Width + Petal.Length,
        data = iris2, kernel = "linear")

# plot data and separating hyperplane
plot(Petal.Length ~ Petal.Width, data = iris2, col = setosa)
(cf <- coef(m))
#>  (Intercept)  Petal.Width Petal.Length 
#>    -1.658953    -1.172523    -1.358030 
abline(-cf[1]/cf[3], -cf[2]/cf[3], col = "red")

# plot margin and mark support vectors
abline(-(cf[1] + 1)/cf[3], -cf[2]/cf[3], col = "blue")
abline(-(cf[1] - 1)/cf[3], -cf[2]/cf[3], col = "blue")
points(m$SV, pch = 5, cex = 2)