Generalized Boosted Regression Modeling (GBM)

Source: R/gbm.R

Fits generalized boosted regression models. For technical details, see the vignette: utils::browseVignettes("gbm").

gbm(formula = formula(data), distribution = "bernoulli",
  data = list(), weights, var.monotone = NULL, n.trees = 100,
  interaction.depth = 1, n.minobsinnode = 10, shrinkage = 0.1,
  bag.fraction = 0.5, train.fraction = 1, cv.folds = 0,
  keep.data = TRUE, verbose = FALSE, class.stratify.cv = NULL,
  n.cores = NULL)

Arguments

formula

A symbolic description of the model to be fit. The formula may include an offset term (e.g. y~offset(n)+x). If keep.data = FALSE in the initial call to gbm then it is the user's responsibility to resupply the offset to gbm.more.
distribution

Either a character string specifying the name of the distribution to use or a list with a component name specifying the distribution and any additional parameters needed. If not specified, gbm will try to guess: if the response has only 2 unique values, bernoulli is assumed; otherwise, if the response is a factor, multinomial is assumed; otherwise, if the response has class "Surv", coxph is assumed; otherwise, gaussian is assumed.

Currently available options are "gaussian" (squared error), "laplace" (absolute loss), "tdist" (t-distribution loss), "bernoulli" (logistic regression for 0-1 outcomes), "huberized" (huberized hinge loss for 0-1 outcomes), classes), "adaboost" (the AdaBoost exponential loss for 0-1 outcomes), "poisson" (count outcomes), "coxph" (right censored observations), "quantile", or "pairwise" (ranking measure using the LambdaMart algorithm).

If quantile regression is specified, distribution must be a list of the form list(name = "quantile", alpha = 0.25) where alpha is the quantile to estimate. The current version's quantile regression method does not handle non-constant weights and will stop.

If "tdist" is specified, the default degrees of freedom is 4 and this can be controlled by specifying distribution = list(name = "tdist", df = DF) where DF is your chosen degrees of freedom.

If "pairwise" regression is specified, distribution must be a list of the form list(name="pairwise",group=...,metric=...,max.rank=...) (metric and max.rank are optional, see below). group is a character vector with the column names of data that jointly indicate the group an instance belongs to (typically a query in Information Retrieval applications). For training, only pairs of instances from the same group and with different target labels can be considered. metric is the IR measure to use, one of

list("conc")

Fraction of concordant pairs; for binary labels, this is equivalent to the Area under the ROC Curve

:

Fraction of concordant pairs; for binary labels, this is equivalent to the Area under the ROC Curve

list("mrr")

Mean reciprocal rank of the highest-ranked positive instance

:

Mean reciprocal rank of the highest-ranked positive instance

list("map")

Mean average precision, a generalization of mrr to multiple positive instances

:

Mean average precision, a generalization of mrr to multiple positive instances

list("ndcg:")

Normalized discounted cumulative gain. The score is the weighted sum (DCG) of the user-supplied target values, weighted by log(rank+1), and normalized to the maximum achievable value. This is the default if the user did not specify a metric.

ndcg and conc allow arbitrary target values, while binary targets 0,1 are expected for map and mrr. For ndcg and mrr, a cut-off can be chosen using a positive integer parameter max.rank. If left unspecified, all ranks are taken into account.

Note that splitting of instances into training and validation sets follows group boundaries and therefore only approximates the specified train.fraction ratio (the same applies to cross-validation folds). Internally, queries are randomly shuffled before training, to avoid bias.

Weights can be used in conjunction with pairwise metrics, however it is assumed that they are constant for instances from the same group.

For details and background on the algorithm, see e.g. Burges (2010).
data

an optional data frame containing the variables in the model. By default the variables are taken from environment(formula), typically the environment from which gbm is called. If keep.data=TRUE in the initial call to gbm then gbm stores a copy with the object. If keep.data=FALSE then subsequent calls to gbm.more must resupply the same dataset. It becomes the user's responsibility to resupply the same data at this point.
weights

an optional vector of weights to be used in the fitting process. Must be positive but do not need to be normalized. If keep.data=FALSE in the initial call to gbm then it is the user's responsibility to resupply the weights to gbm.more.
var.monotone

an optional vector, the same length as the number of predictors, indicating which variables have a monotone increasing (+1), decreasing (-1), or arbitrary (0) relationship with the outcome.
n.trees

Integer specifying the total number of trees to fit. This is equivalent to the number of iterations and the number of basis functions in the additive expansion. Default is 100.
interaction.depth

Integer specifying the maximum depth of each tree (i.e., the highest level of variable interactions allowed). A value of 1 implies an additive model, a value of 2 implies a model with up to 2-way interactions, etc. Default is 1.
n.minobsinnode

Integer specifying the minimum number of observations in the terminal nodes of the trees. Note that this is the actual number of observations, not the total weight.
shrinkage

a shrinkage parameter applied to each tree in the expansion. Also known as the learning rate or step-size reduction; 0.001 to 0.1 usually work, but a smaller learning rate typically requires more trees. Default is 0.1.
bag.fraction

the fraction of the training set observations randomly selected to propose the next tree in the expansion. This introduces randomnesses into the model fit. If bag.fraction < 1 then running the same model twice will result in similar but different fits. gbm uses the R random number generator so set.seed can ensure that the model can be reconstructed. Preferably, the user can save the returned gbm.object using save. Default is 0.5.
train.fraction

The first train.fraction * nrows(data) observations are used to fit the gbm and the remainder are used for computing out-of-sample estimates of the loss function.
cv.folds

Number of cross-validation folds to perform. If cv.folds>1 then gbm, in addition to the usual fit, will perform a cross-validation, calculate an estimate of generalization error returned in cv.error.
keep.data

a logical variable indicating whether to keep the data and an index of the data stored with the object. Keeping the data and index makes subsequent calls to gbm.more faster at the cost of storing an extra copy of the dataset.
verbose

Logical indicating whether or not to print out progress and performance indicators (TRUE). If this option is left unspecified for gbm.more, then it uses verbose from object. Default is FALSE.
class.stratify.cv

Logical indicating whether or not the cross-validation should be stratified by class. Defaults to TRUE for distribution = "multinomial" and is only implemented for "multinomial" and "bernoulli". The purpose of stratifying the cross-validation is to help avoiding situations in which training sets do not contain all classes.
n.cores

The number of CPU cores to use. The cross-validation loop will attempt to send different CV folds off to different cores. If n.cores is not specified by the user, it is guessed using the detectCores function in the parallel package. Note that the documentation for detectCores makes clear that it is not failsafe and could return a spurious number of available cores.

Value

A gbm.object object.

Details

gbm.fit provides the link between R and the C++ gbm engine. gbm is a front-end to gbm.fit that uses the familiar R modeling formulas. However, model.frame is very slow if there are many predictor variables. For power-users with many variables use gbm.fit. For general practice gbm is preferable.

This package implements the generalized boosted modeling framework. Boosting is the process of iteratively adding basis functions in a greedy fashion so that each additional basis function further reduces the selected loss function. This implementation closely follows Friedman's Gradient Boosting Machine (Friedman, 2001).

In addition to many of the features documented in the Gradient Boosting Machine, gbm offers additional features including the out-of-bag estimator for the optimal number of iterations, the ability to store and manipulate the resulting gbm object, and a variety of other loss functions that had not previously had associated boosting algorithms, including the Cox partial likelihood for censored data, the poisson likelihood for count outcomes, and a gradient boosting implementation to minimize the AdaBoost exponential loss function.

References

Y. Freund and R.E. Schapire (1997) “A decision-theoretic generalization of on-line learning and an application to boosting,” Journal of Computer and System Sciences, 55(1):119-139.

G. Ridgeway (1999). “The state of boosting,” Computing Science and Statistics 31:172-181.

J.H. Friedman, T. Hastie, R. Tibshirani (2000). “Additive Logistic Regression: a Statistical View of Boosting,” Annals of Statistics 28(2):337-374.

J.H. Friedman (2001). “Greedy Function Approximation: A Gradient Boosting Machine,” Annals of Statistics 29(5):1189-1232.

J.H. Friedman (2002). “Stochastic Gradient Boosting,” Computational Statistics and Data Analysis 38(4):367-378.

B. Kriegler (2007). Cost-Sensitive Stochastic Gradient Boosting Within a Quantitative Regression Framework. Ph.D. Dissertation. University of California at Los Angeles, Los Angeles, CA, USA. Advisor(s) Richard A. Berk. urlhttps://dl.acm.org/citation.cfm?id=1354603.

C. Burges (2010). “From RankNet to LambdaRank to LambdaMART: An Overview,” Microsoft Research Technical Report MSR-TR-2010-82.

See also

gbm.object, gbm.perf, plot.gbm, predict.gbm, summary.gbm, and pretty.gbm.tree.

Examples

#
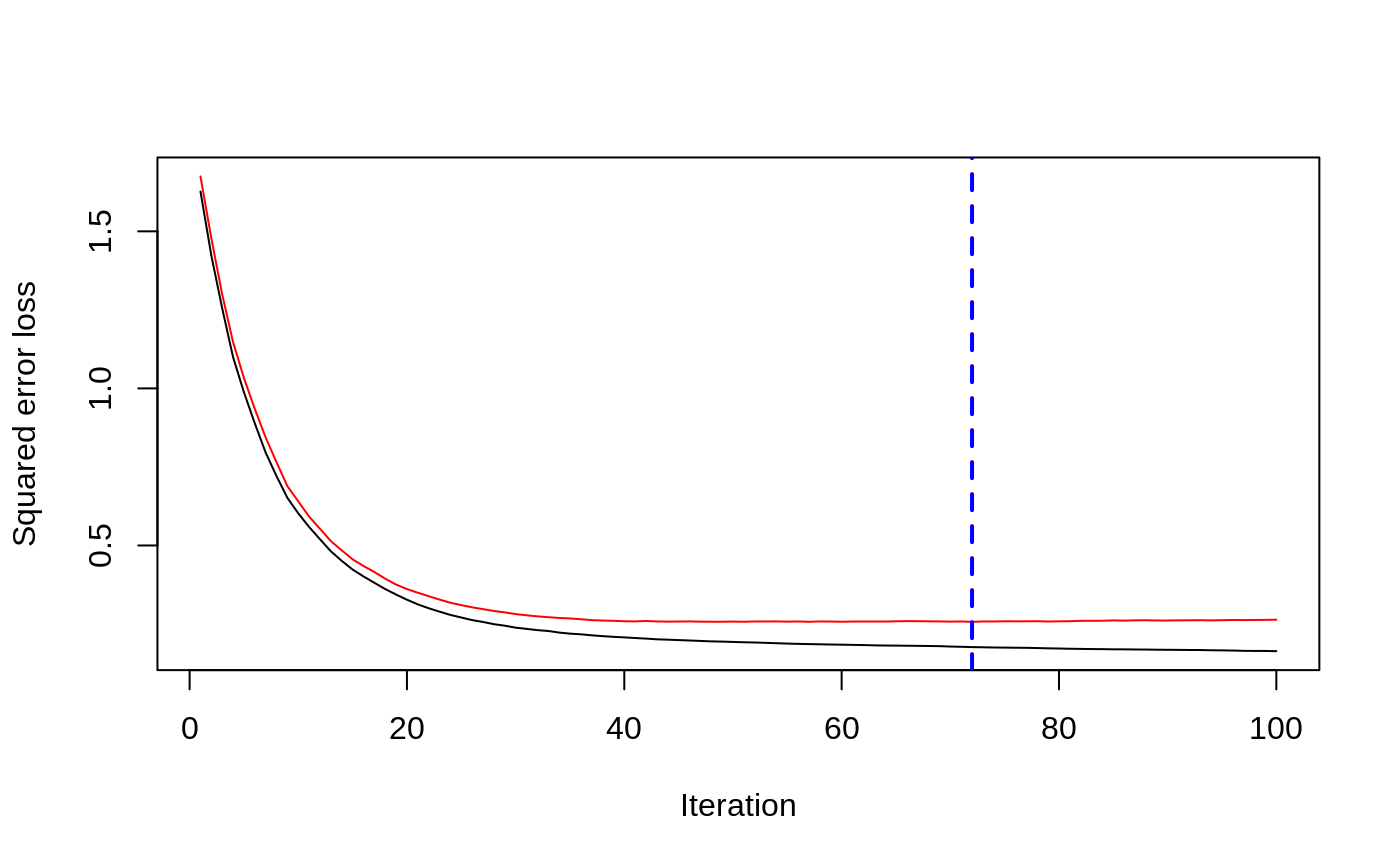
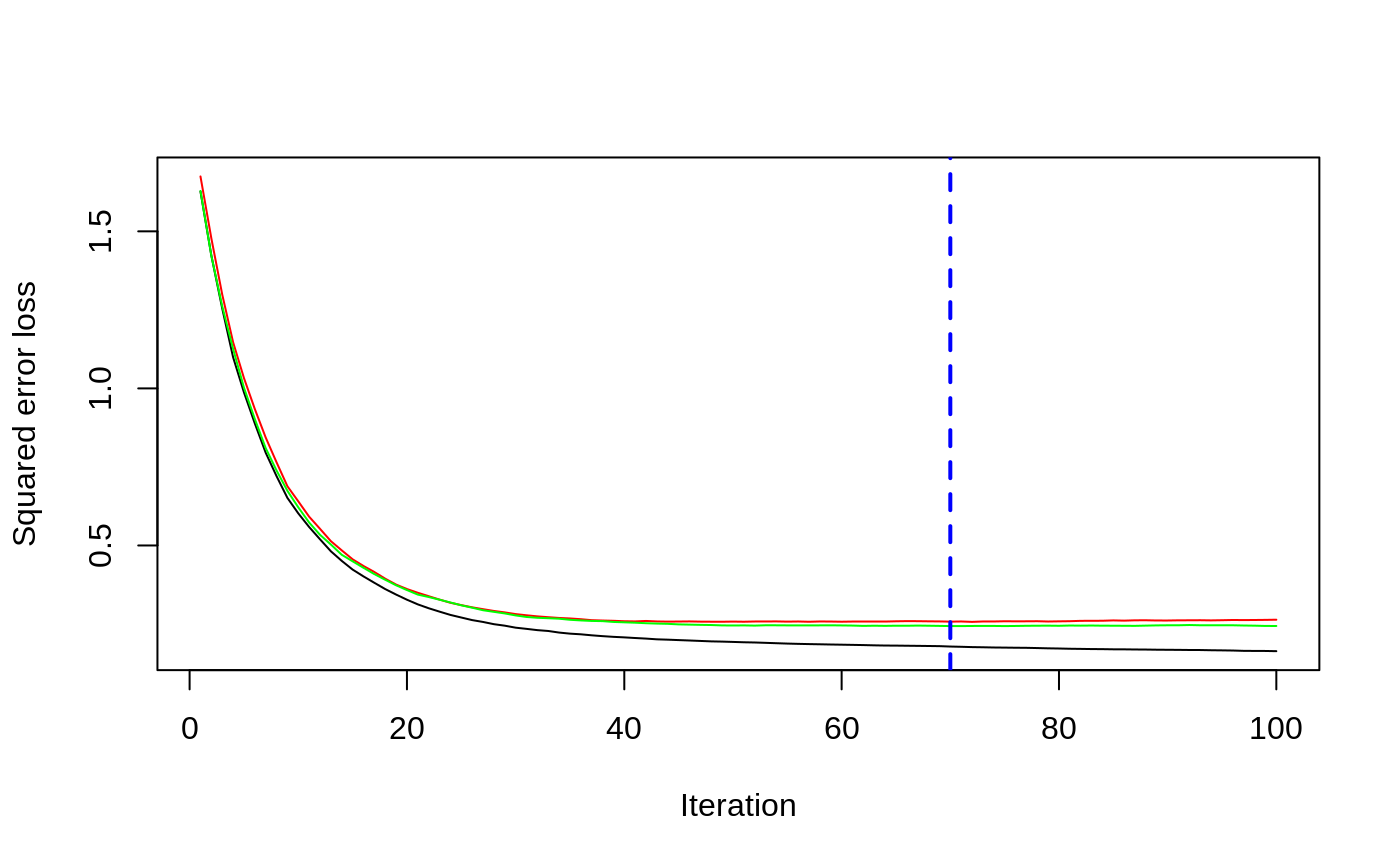
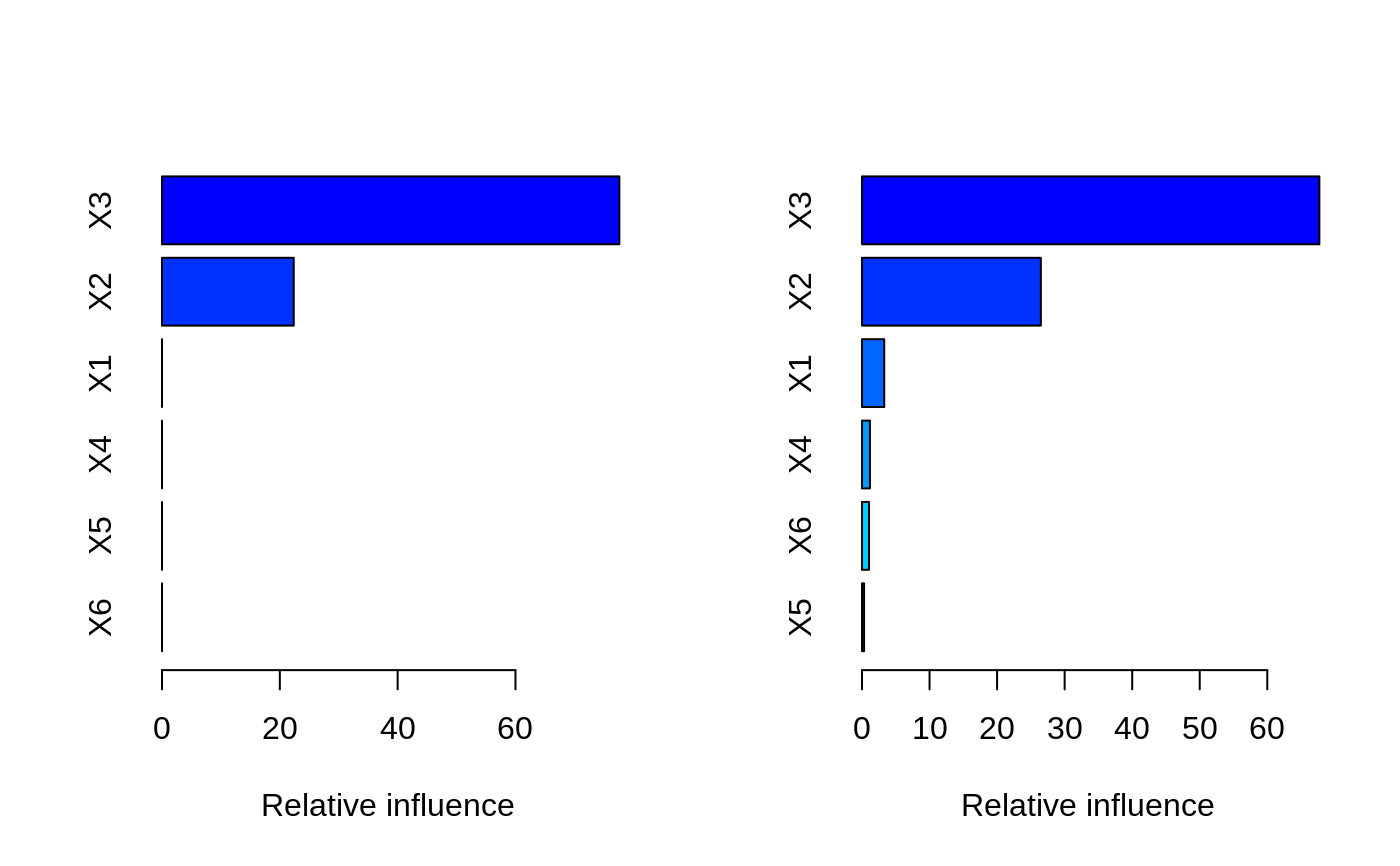
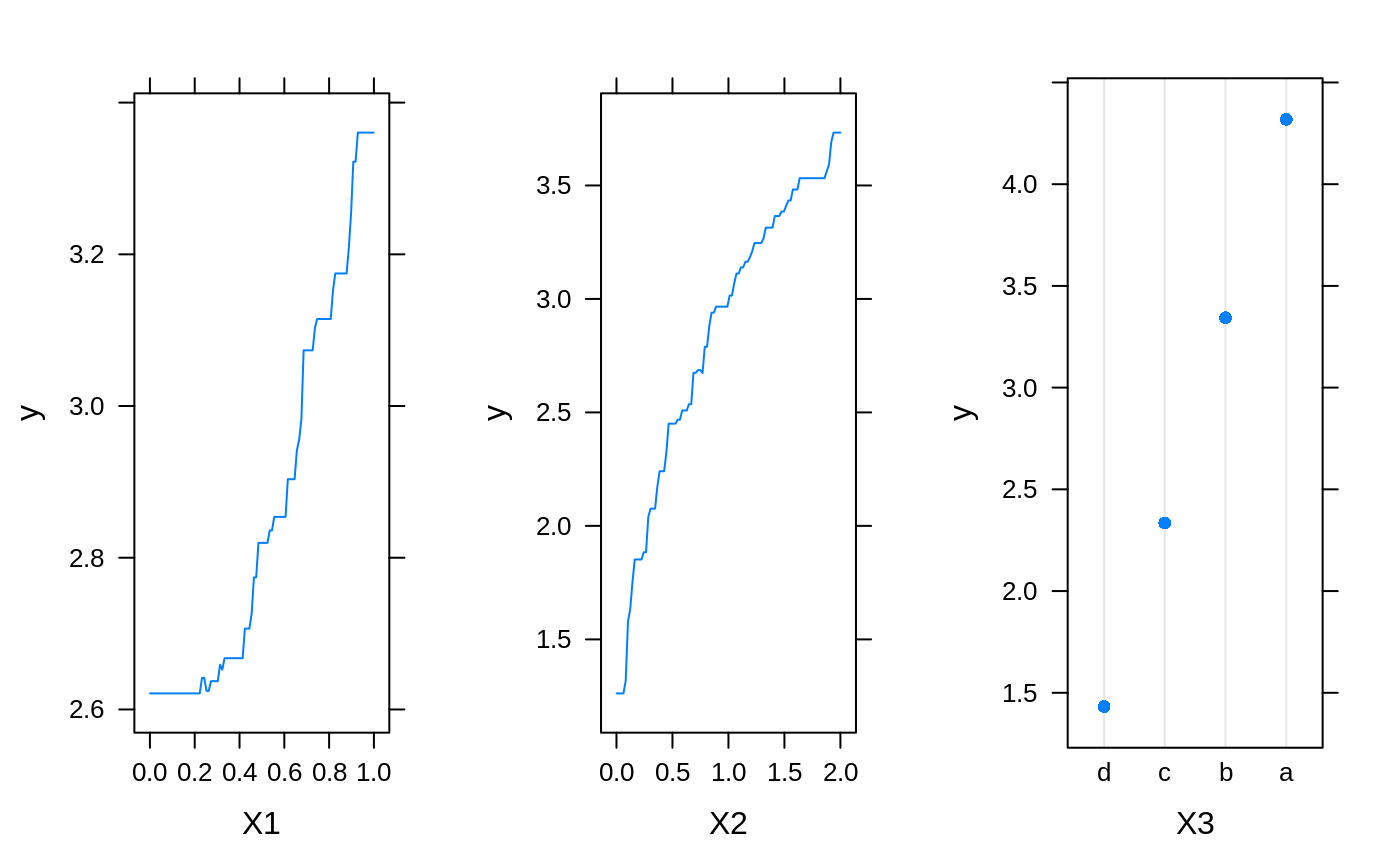
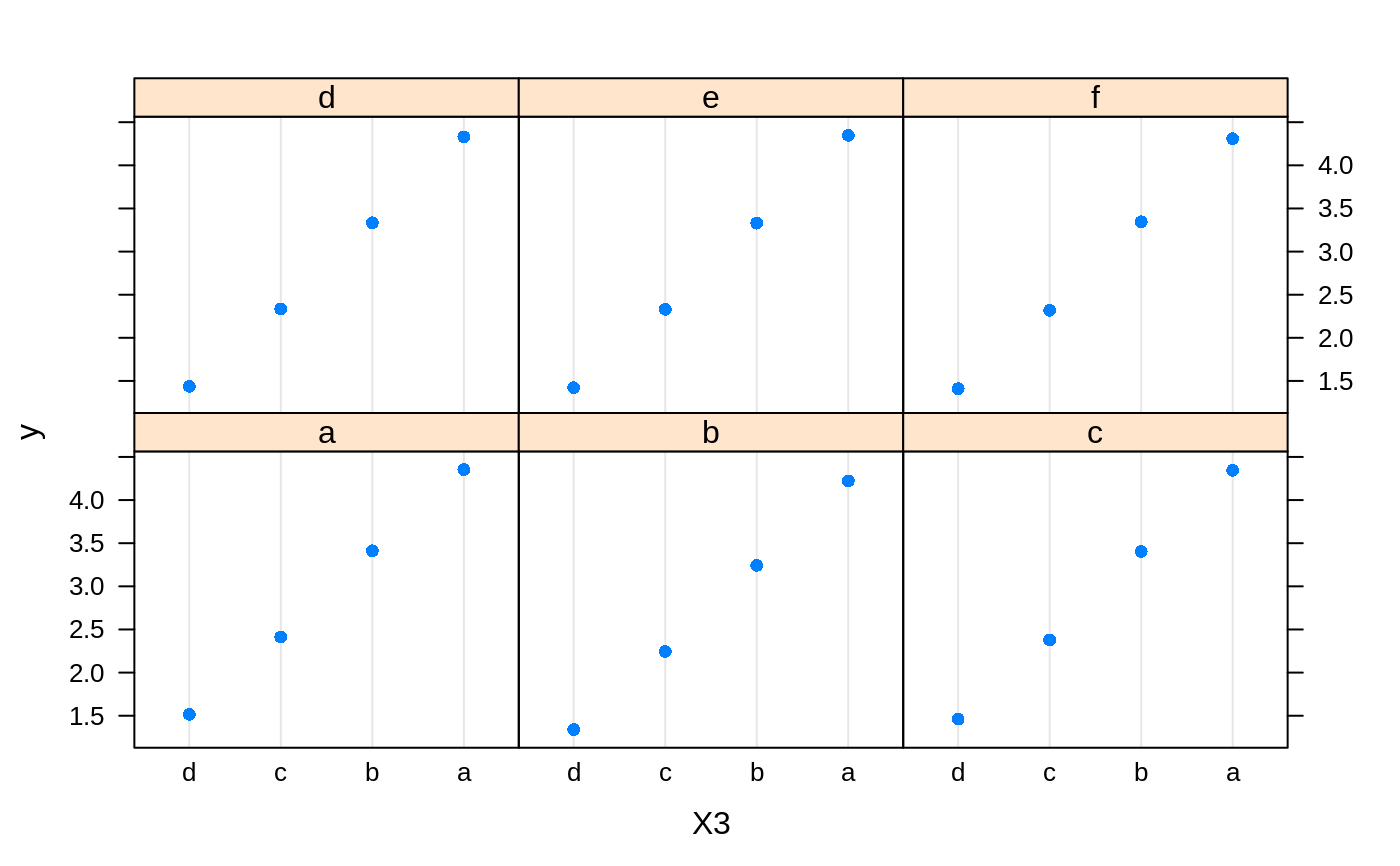
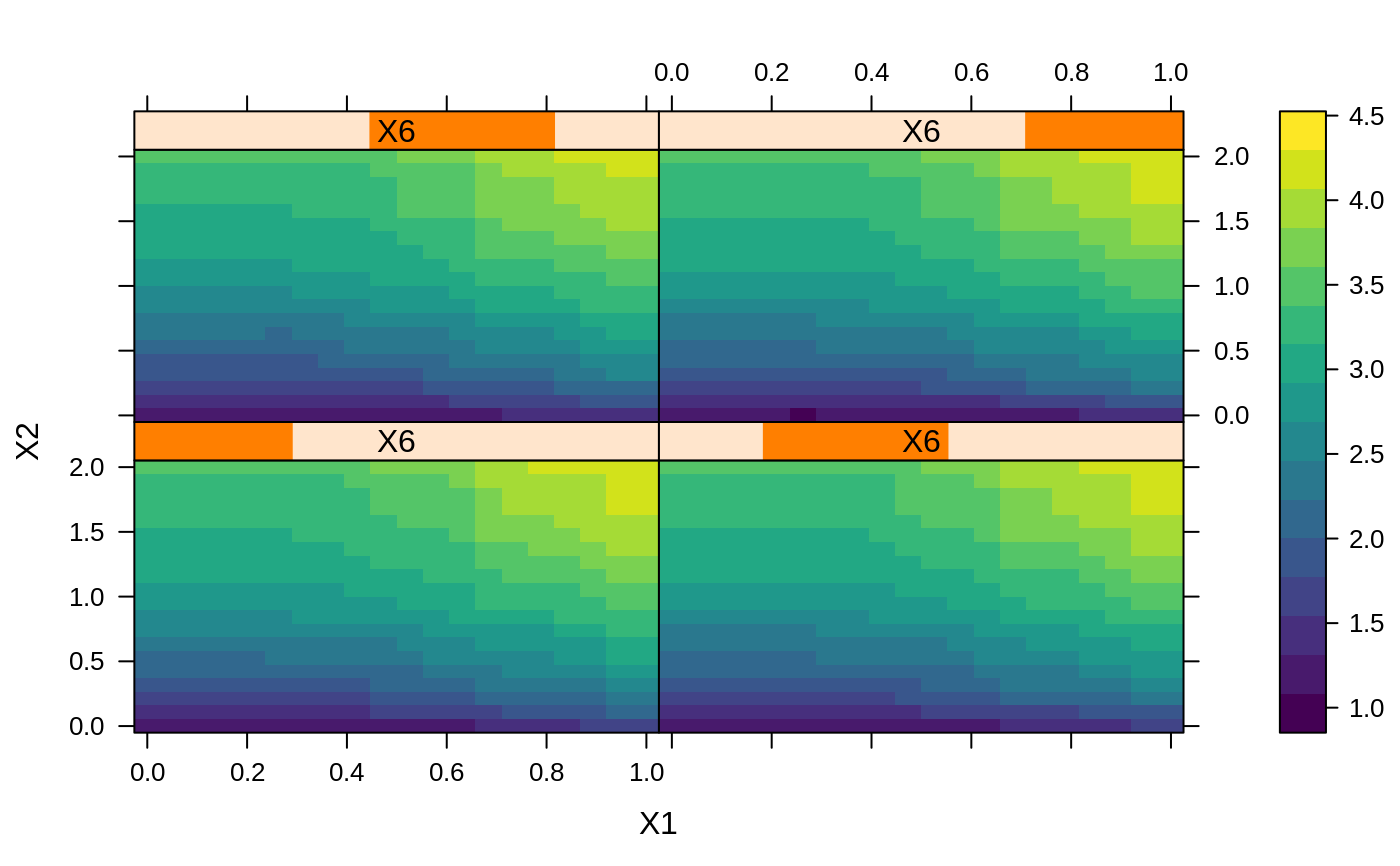
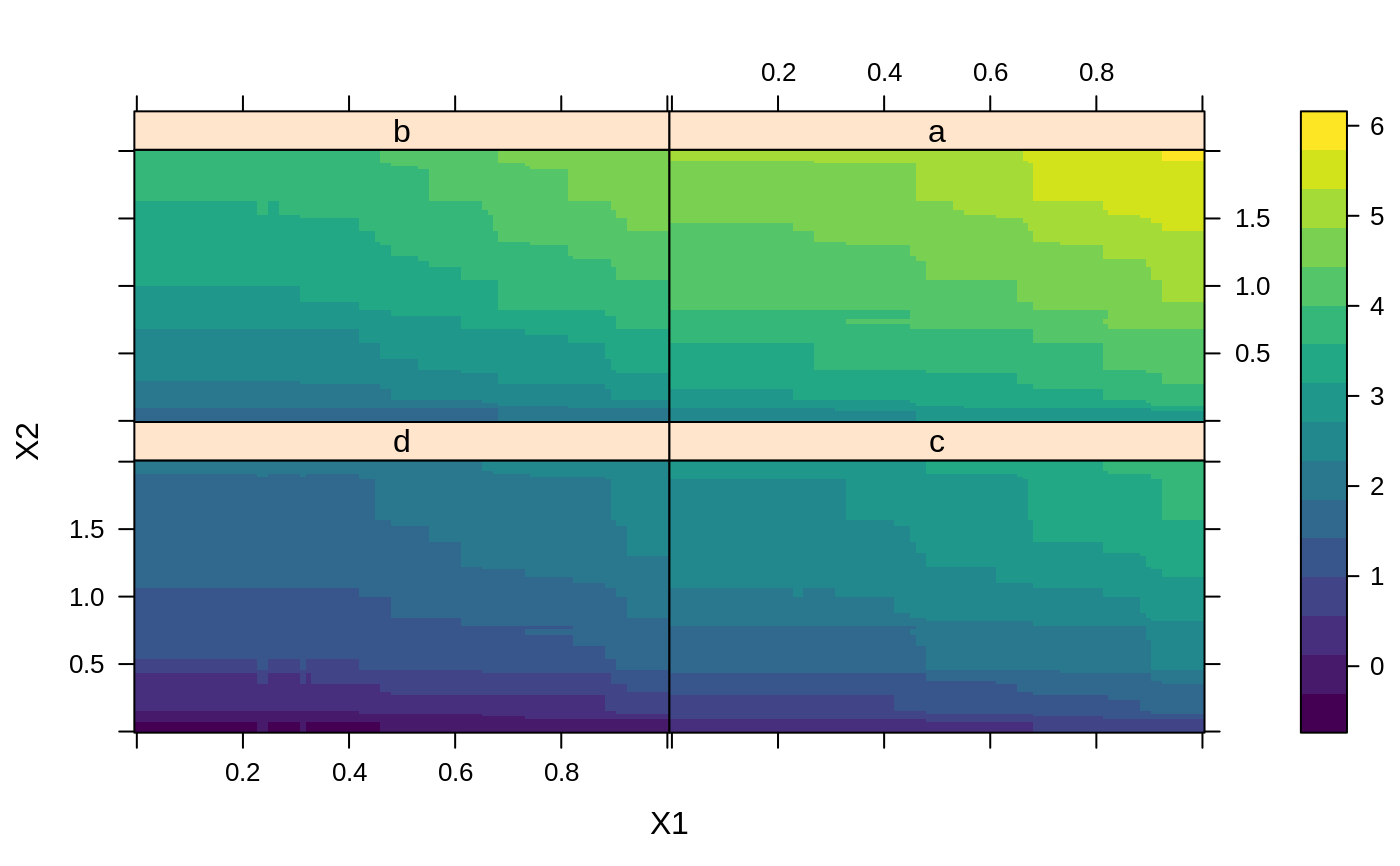
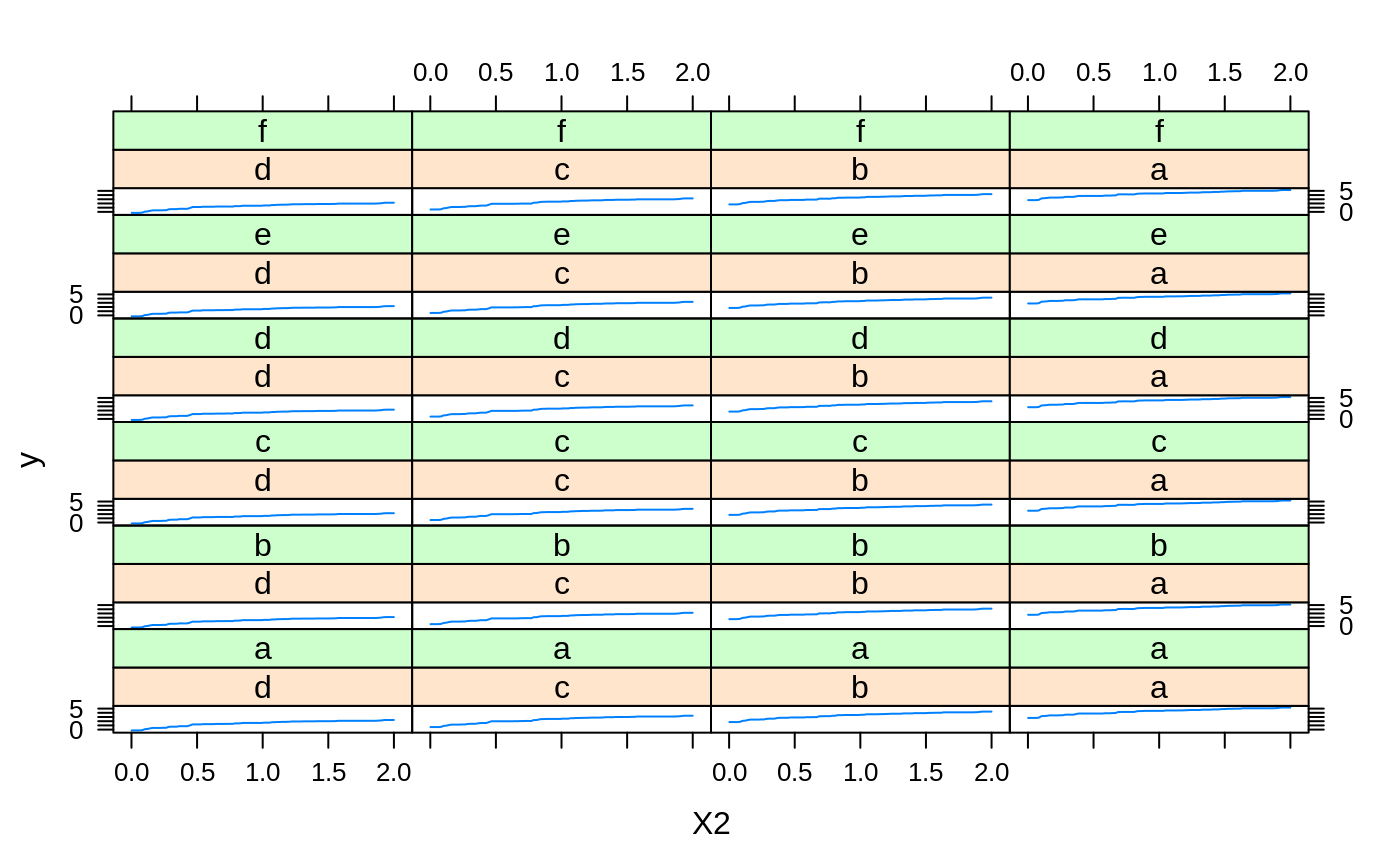
# A least squares regression example 
#

# Simulate data
set.seed(101)  # for reproducibility
N <- 1000
X1 <- runif(N)
X2 <- 2 * runif(N)
X3 <- ordered(sample(letters[1:4], N, replace = TRUE), levels = letters[4:1])
X4 <- factor(sample(letters[1:6], N, replace = TRUE))
X5 <- factor(sample(letters[1:3], N, replace = TRUE))
X6 <- 3 * runif(N)
mu <- c(-1, 0, 1, 2)[as.numeric(X3)]
SNR <- 10  # signal-to-noise ratio
Y <- X1 ^ 1.5 + 2 * (X2 ^ 0.5) + mu
sigma <- sqrt(var(Y) / SNR)
Y <- Y + rnorm(N, 0, sigma)
X1[sample(1:N, size = 500)] <- NA  # introduce some missing values
X4[sample(1:N, size = 300)] <- NA  # introduce some missing values
data <- data.frame(Y, X1, X2, X3, X4, X5, X6)

# Fit a GBM
set.seed(102)  # for reproducibility
gbm1 <- gbm(Y ~ ., data = data, var.monotone = c(0, 0, 0, 0, 0, 0),
            distribution = "gaussian", n.trees = 100, shrinkage = 0.1,
            interaction.depth = 3, bag.fraction = 0.5, train.fraction = 0.5,
            n.minobsinnode = 10, cv.folds = 5, keep.data = TRUE,
            verbose = FALSE, n.cores = 1)

# Check performance using the out-of-bag (OOB) error; the OOB error typically
# underestimates the optimal number of iterations
best.iter <- gbm.perf(gbm1, method = "OOB")
#> OOB generally underestimates the optimal number of iterations although predictive performance is reasonably competitive. Using cv_folds>1 when calling gbm usually results in improved predictive performance.
print(best.iter)
#> [1] 39
#> attr(,"smoother")
#> Call:
#> loess(formula = object$oobag.improve ~ x, enp.target = min(max(4, 
#>     length(x)/10), 50))
#> 
#> Number of Observations: 100 
#> Equivalent Number of Parameters: 8.32 
#> Residual Standard Error: 0.00482 

# Check performance using the 50% heldout test set
best.iter <- gbm.perf(gbm1, method = "test")
print(best.iter)
#> [1] 72

# Check performance using 5-fold cross-validation
best.iter <- gbm.perf(gbm1, method = "cv")
print(best.iter)
#> [1] 70

# Plot relative influence of each variable
par(mfrow = c(1, 2))
summary(gbm1, n.trees = 1)          # using first tree
#>    var  rel.inf
#> X3  X3 77.63653
#> X2  X2 22.36347
#> X1  X1  0.00000
#> X4  X4  0.00000
#> X5  X5  0.00000
#> X6  X6  0.00000
summary(gbm1, n.trees = best.iter)  # using estimated best number of trees
#>    var    rel.inf
#> X3  X3 67.7119268
#> X2  X2 26.4776500
#> X1  X1  3.2894907
#> X4  X4  1.1762229
#> X6  X6  1.0391610
#> X5  X5  0.3055486

# Compactly print the first and last trees for curiosity
print(pretty.gbm.tree(gbm1, i.tree = 1))
#>   SplitVar SplitCodePred LeftNode RightNode MissingNode ErrorReduction Weight
#> 0        2    1.50000000        1         5           9      250.57638    250
#> 1        1    0.78120367        2         3           4       37.35455    126
#> 2       -1   -0.18949436       -1        -1          -1        0.00000     41
#> 3       -1   -0.07328112       -1        -1          -1        0.00000     85
#> 4       -1   -0.11109654       -1        -1          -1        0.00000    126
#> 5        1    1.04599545        6         7           8       34.82483    124
#> 6       -1    0.03528368       -1        -1          -1        0.00000     61
#> 7       -1    0.14128717       -1        -1          -1        0.00000     63
#> 8       -1    0.08914029       -1        -1          -1        0.00000    124
#> 9       -1   -0.01177907       -1        -1          -1        0.00000    250
#>    Prediction
#> 0 -0.01177907
#> 1 -0.11109654
#> 2 -0.18949436
#> 3 -0.07328112
#> 4 -0.11109654
#> 5  0.08914029
#> 6  0.03528368
#> 7  0.14128717
#> 8  0.08914029
#> 9 -0.01177907
print(pretty.gbm.tree(gbm1, i.tree = gbm1$n.trees))
#>   SplitVar SplitCodePred LeftNode RightNode MissingNode ErrorReduction Weight
#> 0        0  0.6583952396        1         2           3      0.5862803    250
#> 1       -1 -0.0005414893       -1        -1          -1      0.0000000     85
#> 2       -1  0.0127684504       -1        -1          -1      0.0000000     44
#> 3        3 48.0000000000        4         5           9      0.6988419    121
#> 4       -1 -0.0120865976       -1        -1          -1      0.0000000     32
#> 5        5  1.2224274612        6         7           8      0.7638308     53
#> 6       -1  0.0285211180       -1        -1          -1      0.0000000     11
#> 7       -1 -0.0010805051       -1        -1          -1      0.0000000     42
#> 8       -1  0.0050632280       -1        -1          -1      0.0000000     53
#> 9       -1  0.0052615051       -1        -1          -1      0.0000000     36
#>      Prediction
#> 0  0.0023471175
#> 1 -0.0005414893
#> 2  0.0127684504
#> 3  0.0005867285
#> 4 -0.0120865976
#> 5  0.0050632280
#> 6  0.0285211180
#> 7 -0.0010805051
#> 8  0.0050632280
#> 9  0.0052615051

# Simulate new data
set.seed(103)  # for reproducibility
N <- 1000
X1 <- runif(N)
X2 <- 2 * runif(N)
X3 <- ordered(sample(letters[1:4], N, replace = TRUE))
X4 <- factor(sample(letters[1:6], N, replace = TRUE))
X5 <- factor(sample(letters[1:3], N, replace = TRUE))
X6 <- 3 * runif(N)
mu <- c(-1, 0, 1, 2)[as.numeric(X3)]
Y <- X1 ^ 1.5 + 2 * (X2 ^ 0.5) + mu + rnorm(N, 0, sigma)
data2 <- data.frame(Y, X1, X2, X3, X4, X5, X6)

# Predict on the new data using the "best" number of trees; by default,
# predictions will be on the link scale
Yhat <- predict(gbm1, newdata = data2, n.trees = best.iter, type = "link")

# least squares error
print(sum((data2$Y - Yhat)^2))
#> [1] 5201.051

# Construct univariate partial dependence plots
p1 <- plot(gbm1, i.var = 1, n.trees = best.iter)
p2 <- plot(gbm1, i.var = 2, n.trees = best.iter)
p3 <- plot(gbm1, i.var = "X3", n.trees = best.iter)  # can use index or name
grid.arrange(p1, p2, p3, ncol = 3)

# Construct bivariate partial dependence plots
plot(gbm1, i.var = 1:2, n.trees = best.iter)
plot(gbm1, i.var = c("X2", "X3"), n.trees = best.iter)
plot(gbm1, i.var = 3:4, n.trees = best.iter)

# Construct trivariate partial dependence plots
plot(gbm1, i.var = c(1, 2, 6), n.trees = best.iter,
     continuous.resolution = 20)
plot(gbm1, i.var = 1:3, n.trees = best.iter)
plot(gbm1, i.var = 2:4, n.trees = best.iter)
plot(gbm1, i.var = 3:5, n.trees = best.iter)

# Add more (i.e., 100) boosting iterations to the ensemble
gbm2 <- gbm.more(gbm1, n.new.trees = 100, verbose = FALSE)