Generalized Boosted Regression Modeling (GBM)

Source: R/gbm.more.R

Adds additional trees to a gbm.object object.

gbm.more(object, n.new.trees = 100, data = NULL, weights = NULL,
  offset = NULL, verbose = NULL)

Arguments

object

A gbm.object object created from an initial call to gbm.
n.new.trees

Integer specifying the number of additional trees to add to object. Default is 100.
data

An optional data frame containing the variables in the model. By default the variables are taken from environment(formula), typically the environment from which gbm is called. If keep.data=TRUE in the initial call to gbm then gbm stores a copy with the object. If keep.data=FALSE then subsequent calls to gbm.more must resupply the same dataset. It becomes the user's responsibility to resupply the same data at this point.
weights

An optional vector of weights to be used in the fitting process. Must be positive but do not need to be normalized. If keep.data=FALSE in the initial call to gbm then it is the user's responsibility to resupply the weights to gbm.more.
offset

A vector of offset values.
verbose

Logical indicating whether or not to print out progress and performance indicators (TRUE). If this option is left unspecified for gbm.more, then it uses verbose from object. Default is FALSE.

Value

A gbm.object object.

Examples

#
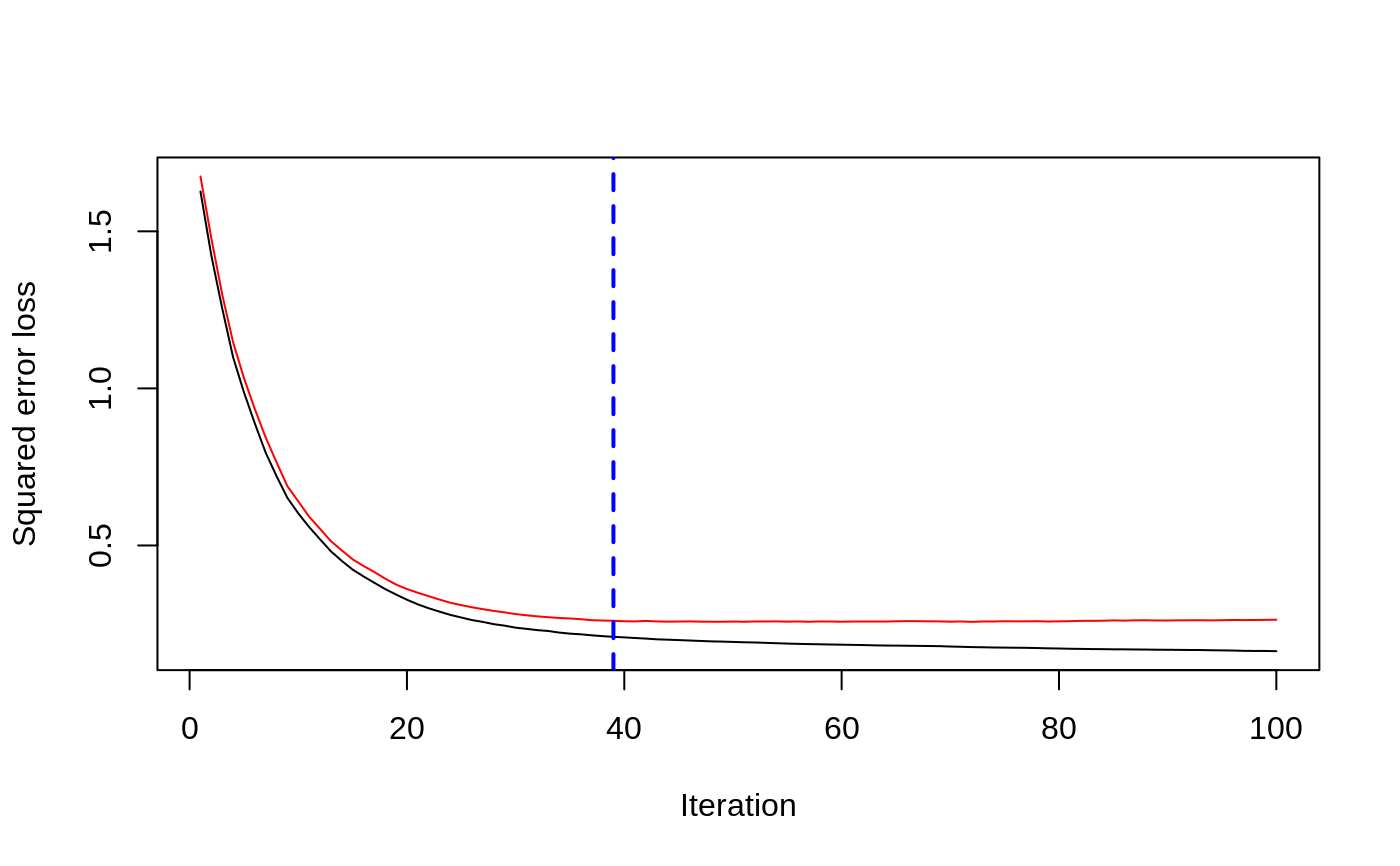
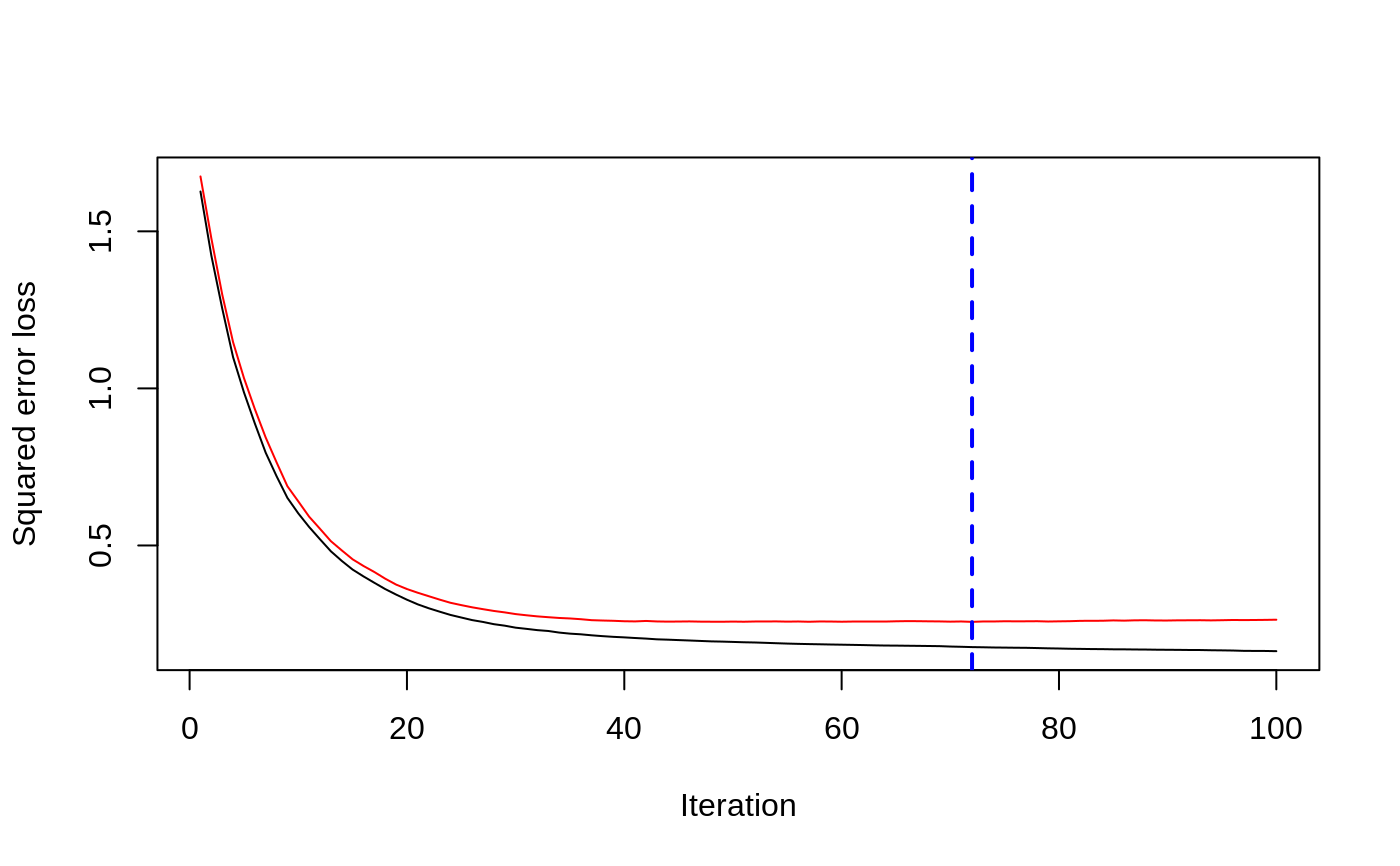
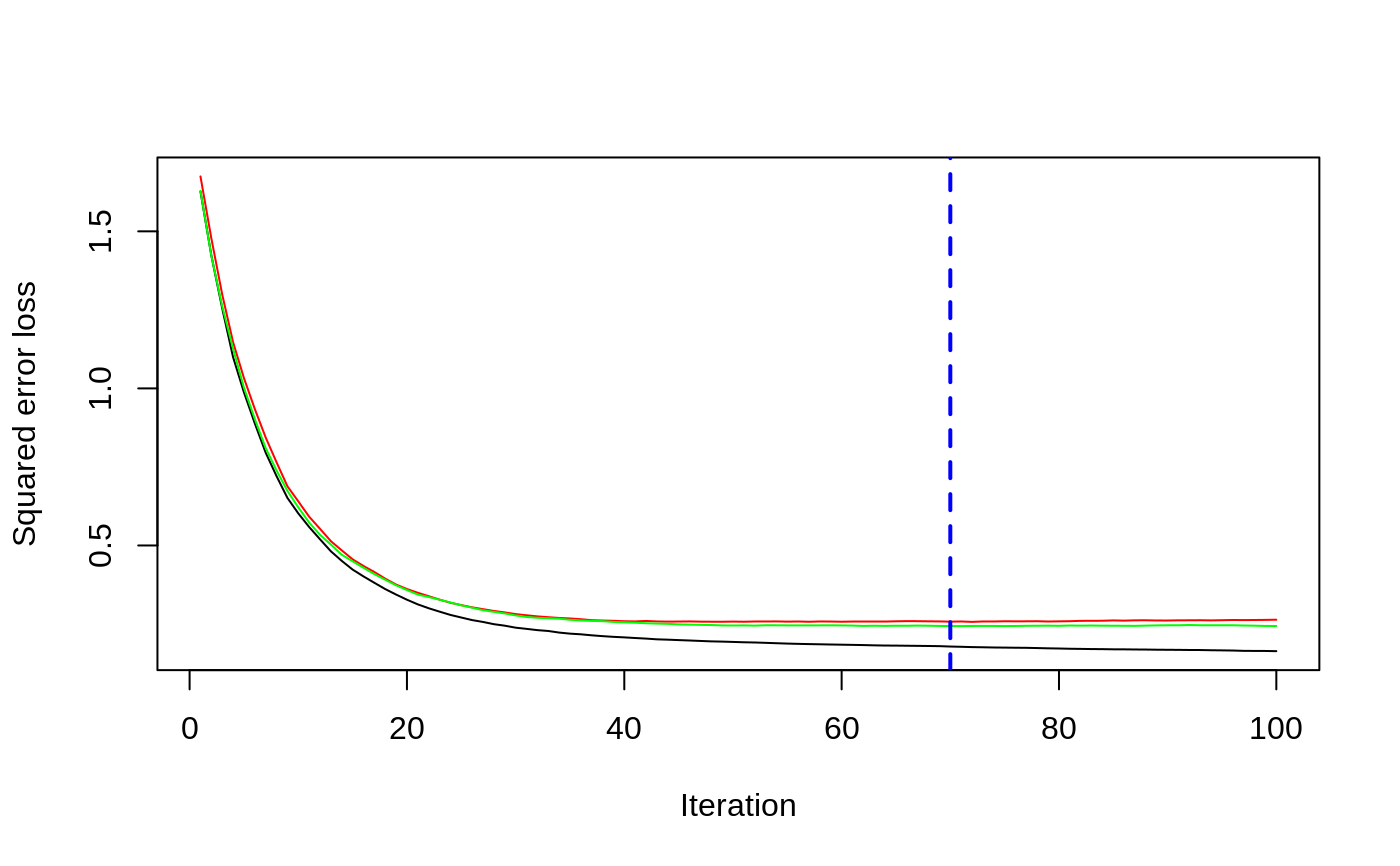
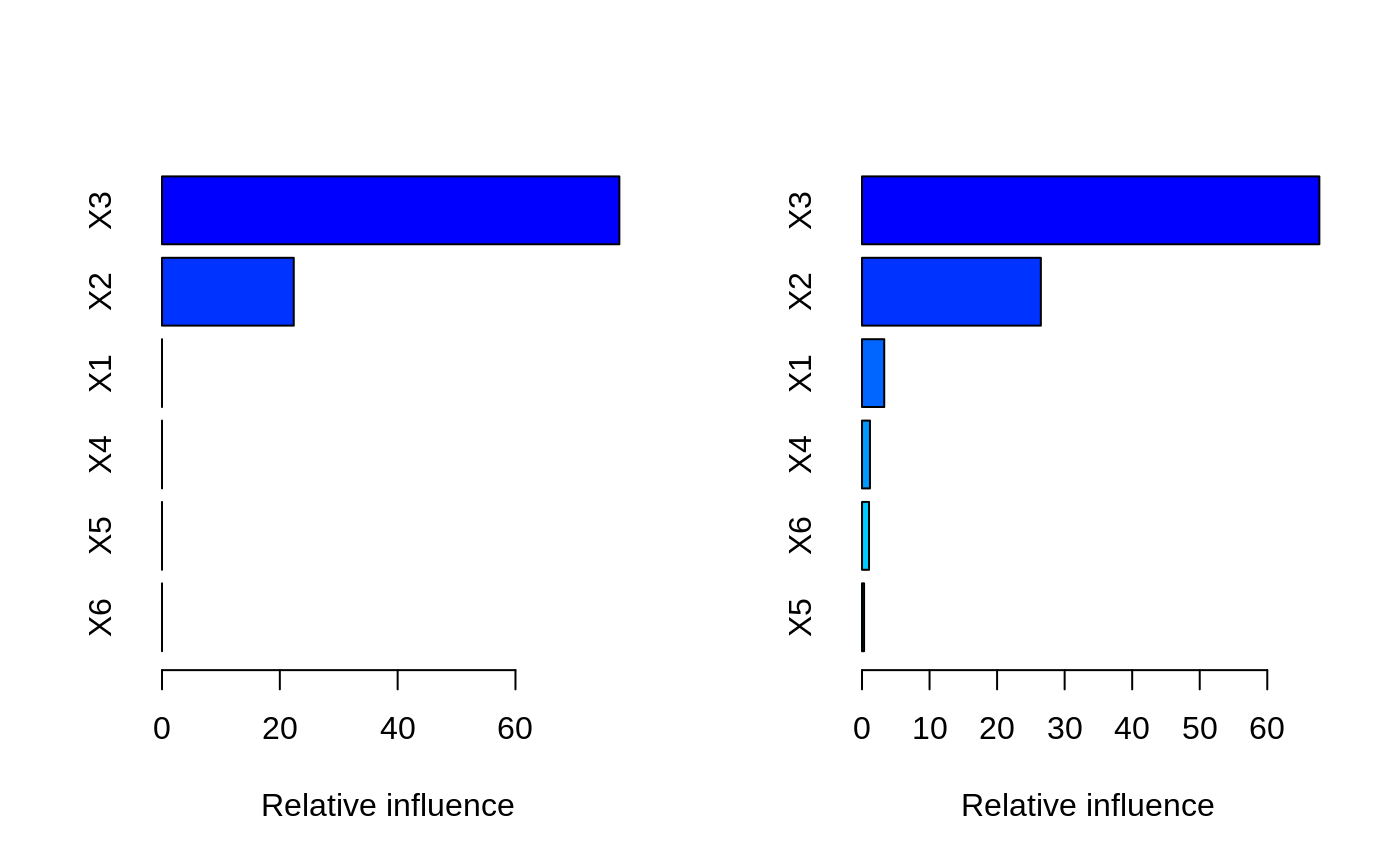
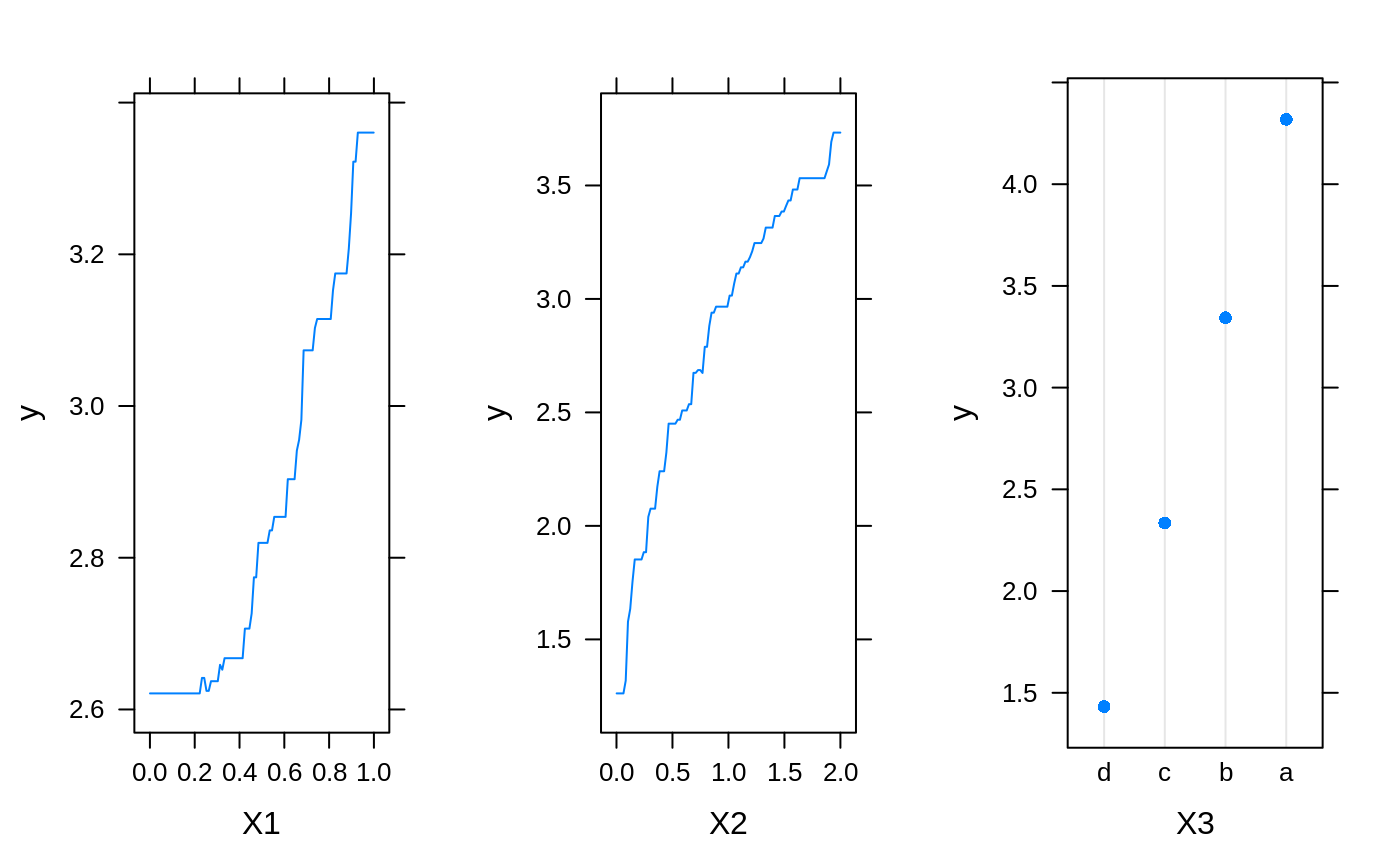
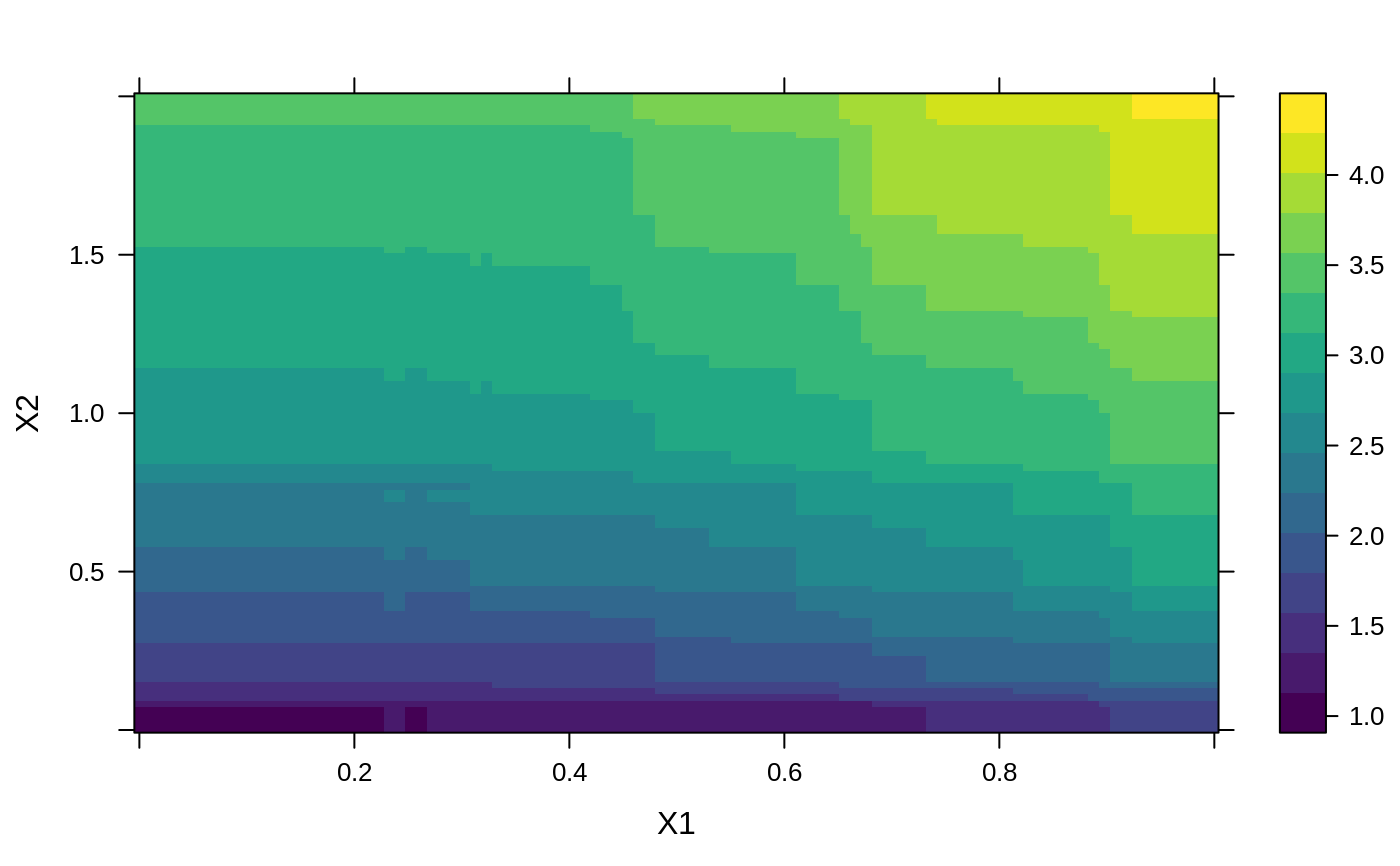
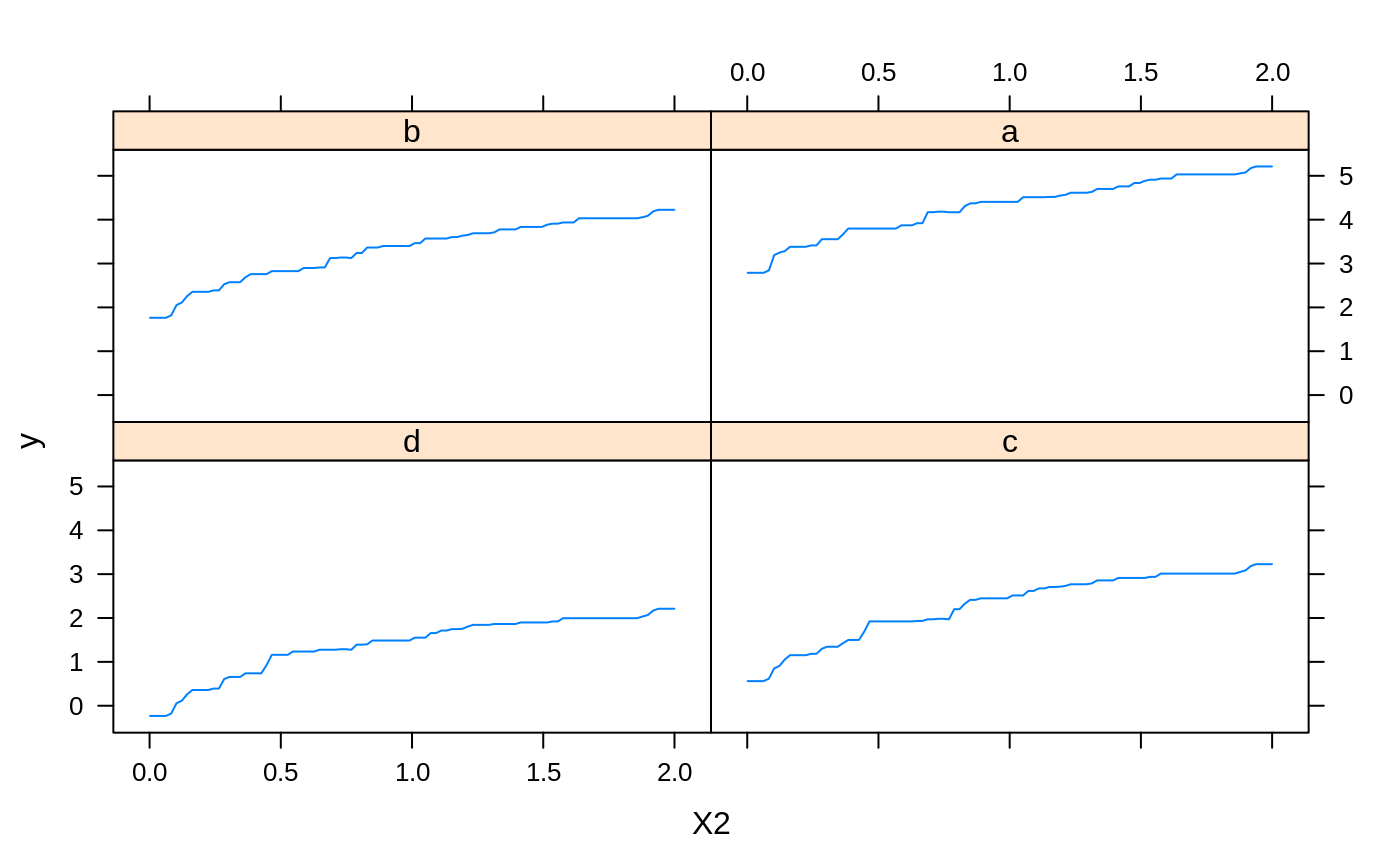
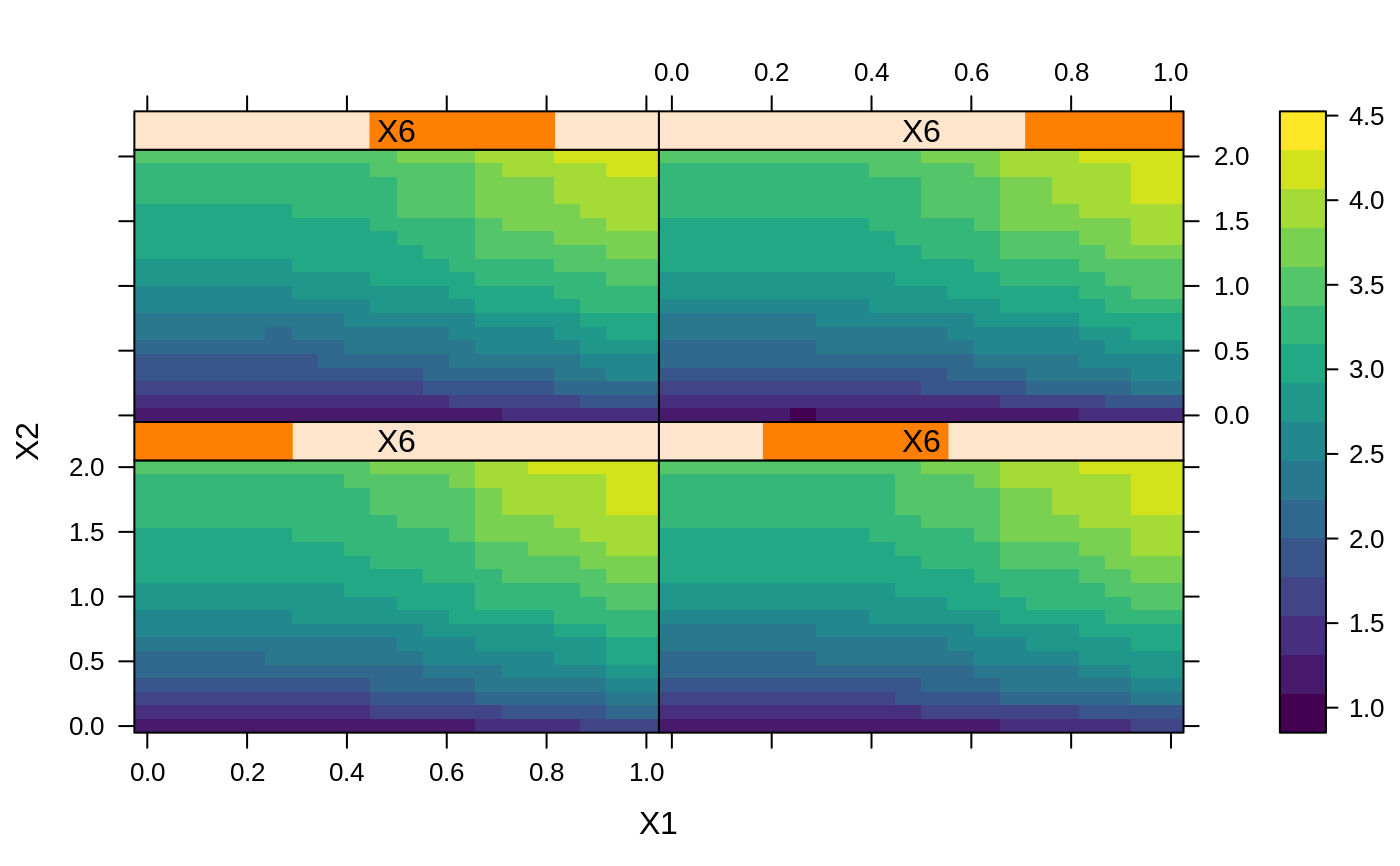
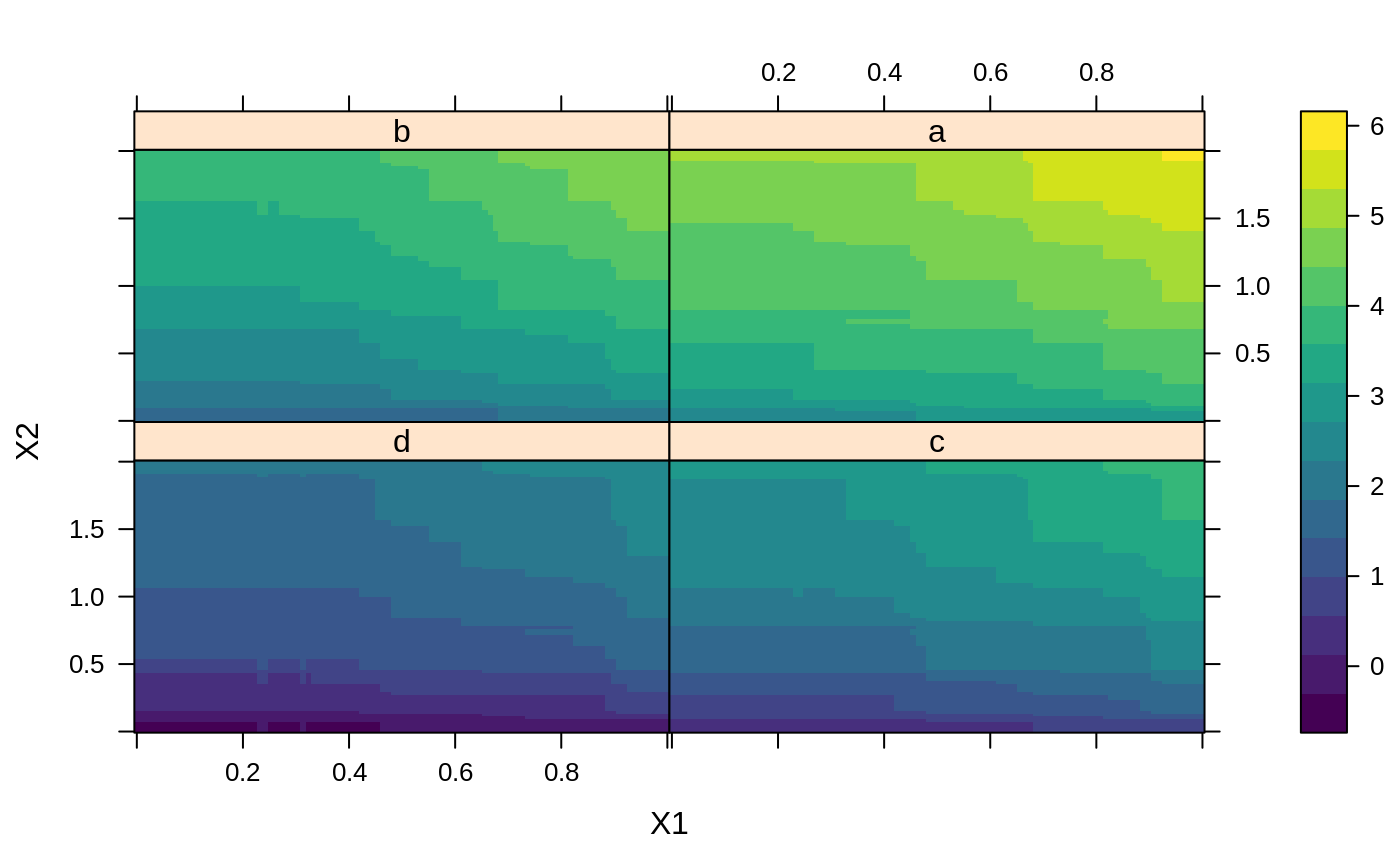
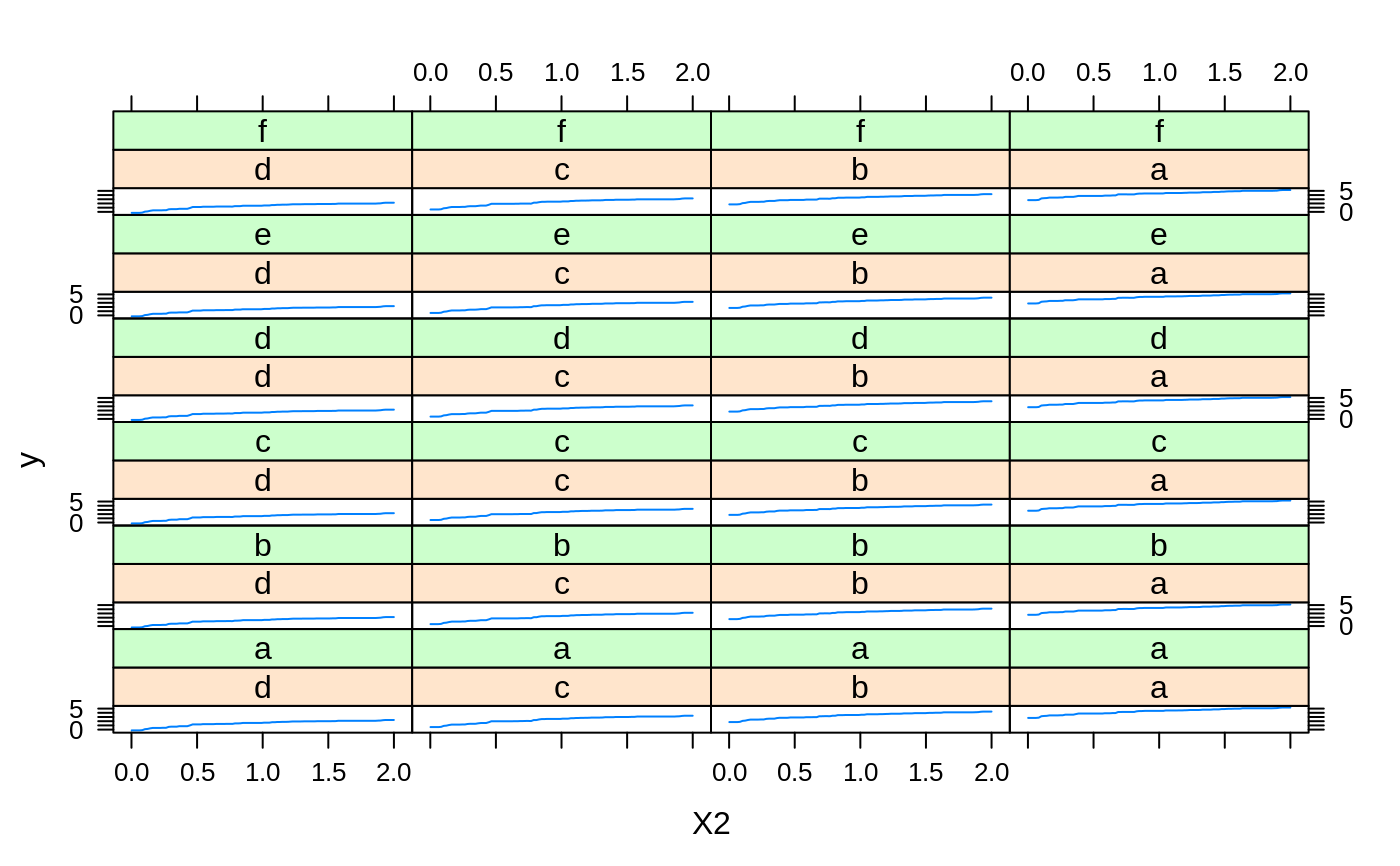
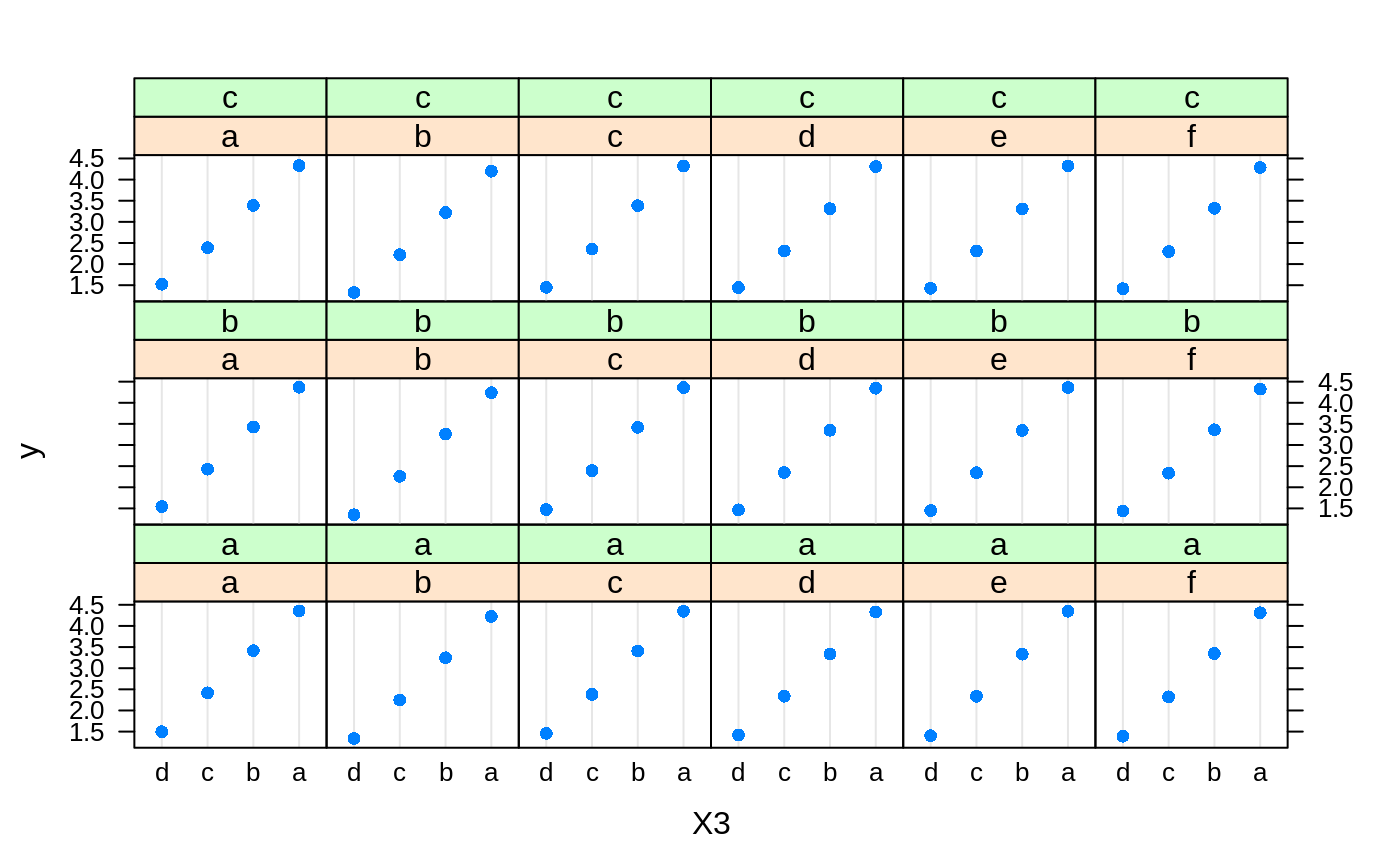
# A least squares regression example 
#

# Simulate data
set.seed(101)  # for reproducibility
N <- 1000
X1 <- runif(N)
X2 <- 2 * runif(N)
X3 <- ordered(sample(letters[1:4], N, replace = TRUE), levels = letters[4:1])
X4 <- factor(sample(letters[1:6], N, replace = TRUE))
X5 <- factor(sample(letters[1:3], N, replace = TRUE))
X6 <- 3 * runif(N)
mu <- c(-1, 0, 1, 2)[as.numeric(X3)]
SNR <- 10  # signal-to-noise ratio
Y <- X1 ^ 1.5 + 2 * (X2 ^ 0.5) + mu
sigma <- sqrt(var(Y) / SNR)
Y <- Y + rnorm(N, 0, sigma)
X1[sample(1:N,size=500)] <- NA  # introduce some missing values
X4[sample(1:N,size=300)] <- NA  # introduce some missing values
data <- data.frame(Y, X1, X2, X3, X4, X5, X6)

# Fit a GBM
set.seed(102)  # for reproducibility
gbm1 <- gbm(Y ~ ., data = data, var.monotone = c(0, 0, 0, 0, 0, 0),
            distribution = "gaussian", n.trees = 100, shrinkage = 0.1,
            interaction.depth = 3, bag.fraction = 0.5, train.fraction = 0.5,
            n.minobsinnode = 10, cv.folds = 5, keep.data = TRUE,
            verbose = FALSE, n.cores = 1)

# Check performance using the out-of-bag (OOB) error; the OOB error typically
# underestimates the optimal number of iterations
best.iter <- gbm.perf(gbm1, method = "OOB")
#> OOB generally underestimates the optimal number of iterations although predictive performance is reasonably competitive. Using cv_folds>1 when calling gbm usually results in improved predictive performance.
print(best.iter)
#> [1] 39
#> attr(,"smoother")
#> Call:
#> loess(formula = object$oobag.improve ~ x, enp.target = min(max(4, 
#>     length(x)/10), 50))
#> 
#> Number of Observations: 100 
#> Equivalent Number of Parameters: 8.32 
#> Residual Standard Error: 0.00482 

# Check performance using the 50% heldout test set
best.iter <- gbm.perf(gbm1, method = "test")
print(best.iter)
#> [1] 72

# Check performance using 5-fold cross-validation
best.iter <- gbm.perf(gbm1, method = "cv")
print(best.iter)
#> [1] 70

# Plot relative influence of each variable
par(mfrow = c(1, 2))
summary(gbm1, n.trees = 1)          # using first tree
#>    var  rel.inf
#> X3  X3 77.63653
#> X2  X2 22.36347
#> X1  X1  0.00000
#> X4  X4  0.00000
#> X5  X5  0.00000
#> X6  X6  0.00000
summary(gbm1, n.trees = best.iter)  # using estimated best number of trees
#>    var    rel.inf
#> X3  X3 67.7119268
#> X2  X2 26.4776500
#> X1  X1  3.2894907
#> X4  X4  1.1762229
#> X6  X6  1.0391610
#> X5  X5  0.3055486

# Compactly print the first and last trees for curiosity
print(pretty.gbm.tree(gbm1, i.tree = 1))
#>   SplitVar SplitCodePred LeftNode RightNode MissingNode ErrorReduction Weight
#> 0        2    1.50000000        1         5           9      250.57638    250
#> 1        1    0.78120367        2         3           4       37.35455    126
#> 2       -1   -0.18949436       -1        -1          -1        0.00000     41
#> 3       -1   -0.07328112       -1        -1          -1        0.00000     85
#> 4       -1   -0.11109654       -1        -1          -1        0.00000    126
#> 5        1    1.04599545        6         7           8       34.82483    124
#> 6       -1    0.03528368       -1        -1          -1        0.00000     61
#> 7       -1    0.14128717       -1        -1          -1        0.00000     63
#> 8       -1    0.08914029       -1        -1          -1        0.00000    124
#> 9       -1   -0.01177907       -1        -1          -1        0.00000    250
#>    Prediction
#> 0 -0.01177907
#> 1 -0.11109654
#> 2 -0.18949436
#> 3 -0.07328112
#> 4 -0.11109654
#> 5  0.08914029
#> 6  0.03528368
#> 7  0.14128717
#> 8  0.08914029
#> 9 -0.01177907
print(pretty.gbm.tree(gbm1, i.tree = gbm1$n.trees))
#>   SplitVar SplitCodePred LeftNode RightNode MissingNode ErrorReduction Weight
#> 0        0  0.6583952396        1         2           3      0.5862803    250
#> 1       -1 -0.0005414893       -1        -1          -1      0.0000000     85
#> 2       -1  0.0127684504       -1        -1          -1      0.0000000     44
#> 3        3 48.0000000000        4         5           9      0.6988419    121
#> 4       -1 -0.0120865976       -1        -1          -1      0.0000000     32
#> 5        5  1.2224274612        6         7           8      0.7638308     53
#> 6       -1  0.0285211180       -1        -1          -1      0.0000000     11
#> 7       -1 -0.0010805051       -1        -1          -1      0.0000000     42
#> 8       -1  0.0050632280       -1        -1          -1      0.0000000     53
#> 9       -1  0.0052615051       -1        -1          -1      0.0000000     36
#>      Prediction
#> 0  0.0023471175
#> 1 -0.0005414893
#> 2  0.0127684504
#> 3  0.0005867285
#> 4 -0.0120865976
#> 5  0.0050632280
#> 6  0.0285211180
#> 7 -0.0010805051
#> 8  0.0050632280
#> 9  0.0052615051

# Simulate new data
set.seed(103)  # for reproducibility
N <- 1000
X1 <- runif(N)
X2 <- 2 * runif(N)
X3 <- ordered(sample(letters[1:4], N, replace = TRUE))
X4 <- factor(sample(letters[1:6], N, replace = TRUE))
X5 <- factor(sample(letters[1:3], N, replace = TRUE))
X6 <- 3 * runif(N)
mu <- c(-1, 0, 1, 2)[as.numeric(X3)]
Y <- X1 ^ 1.5 + 2 * (X2 ^ 0.5) + mu + rnorm(N, 0, sigma)
data2 <- data.frame(Y, X1, X2, X3, X4, X5, X6)

# Predict on the new data using the "best" number of trees; by default,
# predictions will be on the link scale
Yhat <- predict(gbm1, newdata = data2, n.trees = best.iter, type = "link")

# least squares error
print(sum((data2$Y - Yhat)^2))
#> [1] 5201.051

# Construct univariate partial dependence plots
p1 <- plot(gbm1, i.var = 1, n.trees = best.iter)
p2 <- plot(gbm1, i.var = 2, n.trees = best.iter)
p3 <- plot(gbm1, i.var = "X3", n.trees = best.iter)  # can use index or name
grid.arrange(p1, p2, p3, ncol = 3)

# Construct bivariate partial dependence plots
plot(gbm1, i.var = 1:2, n.trees = best.iter)
plot(gbm1, i.var = c("X2", "X3"), n.trees = best.iter)
plot(gbm1, i.var = 3:4, n.trees = best.iter)

# Construct trivariate partial dependence plots
plot(gbm1, i.var = c(1, 2, 6), n.trees = best.iter,
     continuous.resolution = 20)
plot(gbm1, i.var = 1:3, n.trees = best.iter)
plot(gbm1, i.var = 2:4, n.trees = best.iter)
plot(gbm1, i.var = 3:5, n.trees = best.iter)

# Add more (i.e., 100) boosting iterations to the ensemble
gbm2 <- gbm.more(gbm1, n.new.trees = 100, verbose = FALSE)