Probabilistic Programming in Python
Rendered: Dec 31, 2019
PyMC3
This is an example of running PyMC3 inside this project’s docker container. This example is taken from Hierarchical Binominal Model: Rat Tumor Example. Please visit the site to see the complete example.
Example
Data
%matplotlib inline
import pymc3 as pm
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import pymc3.distributions.transforms as tr
import theano.tensor as tt
from scipy.special import gammaln
plt.style.use('seaborn-darkgrid')
print('Running on PyMC3 v{}'.format(pm.__version__))Running on PyMC3 v3.8# rat data (BDA3, p. 102)
y = np.array([
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1,
1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 5, 2,
5, 3, 2, 7, 7, 3, 3, 2, 9, 10, 4, 4, 4, 4, 4, 4, 4,
10, 4, 4, 4, 5, 11, 12, 5, 5, 6, 5, 6, 6, 6, 6, 16, 15,
15, 9, 4
])
n = np.array([
20, 20, 20, 20, 20, 20, 20, 19, 19, 19, 19, 18, 18, 17, 20, 20, 20,
20, 19, 19, 18, 18, 25, 24, 23, 20, 20, 20, 20, 20, 20, 10, 49, 19,
46, 27, 17, 49, 47, 20, 20, 13, 48, 50, 20, 20, 20, 20, 20, 20, 20,
48, 19, 19, 19, 22, 46, 49, 20, 20, 23, 19, 22, 20, 20, 20, 52, 46,
47, 24, 14
])
N = len(n)Model
# Compute on log scale because products turn to sums
def log_likelihood(alpha, beta, y, n):
LL = 0
# Summing over data
for Y, N in zip(y, n):
LL += gammaln(alpha+beta) - gammaln(alpha) - gammaln(beta) + \
gammaln(alpha+Y) + gammaln(beta+N-Y) - gammaln(alpha+beta+N)
return LL
def log_prior(A, B):
return -5/2*np.log(A+B)
def trans_to_beta(x, y):
return np.exp(y)/(np.exp(x)+1)
def trans_to_alpha(x, y):
return np.exp(x)*trans_to_beta(x, y)
# Create space for the parameterization in which we wish to plot
X, Z = np.meshgrid(np.arange(-2.3, -1.3, 0.01), np.arange(1, 5, 0.01))
param_space = np.c_[X.ravel(), Z.ravel()]
df = pd.DataFrame(param_space, columns=['X', 'Z'])
# Transform the space back to alpha beta to compute the log-posterior
df['alpha'] = trans_to_alpha(df.X, df.Z)
df['beta'] = trans_to_beta(df.X, df.Z)
df['log_posterior'] = log_prior(
df.alpha, df.beta) + log_likelihood(df.alpha, df.beta, y, n)
df['log_jacobian'] = np.log(df.alpha) + np.log(df.beta)
df['transformed'] = df.log_posterior+df.log_jacobian
df['exp_trans'] = np.exp(df.transformed - df.transformed.max())
# This will ensure the density is normalized
df['normed_exp_trans'] = df.exp_trans/df.exp_trans.sum()
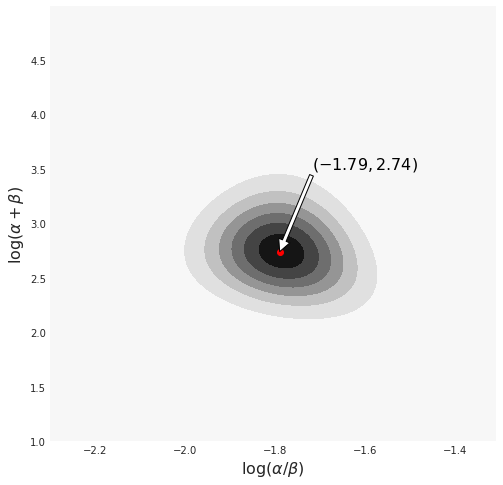
surface = df.set_index(['X', 'Z']).exp_trans.unstack().values.Tfig, ax = plt.subplots(figsize=(8, 8))
ax.contourf(X, Z, surface)
ax.set_xlabel(r'$\log(\alpha/\beta)$', fontsize=16)
ax.set_ylabel(r'$\log(\alpha+\beta)$', fontsize=16)
ix_z, ix_x = np.unravel_index(np.argmax(surface, axis=None), surface.shape)
ax.scatter([X[0, ix_x]], [Z[ix_z, 0]], color='red')
text = r"$({a},{b})$".format(a=np.round(
X[0, ix_x], 2), b=np.round(Z[ix_z, 0], 2))
ax.annotate(text,
xy=(X[0, ix_x], Z[ix_z, 0]),
xytext=(-1.6, 3.5),
ha='center',
fontsize=16,
color='black',
arrowprops={'facecolor':'white'}
);
png
2.40314.319Computing the Posterior using PyMC3
def logp_ab(value):
''' prior density'''
return tt.log(tt.pow(tt.sum(value), -5/2))
with pm.Model() as model:
# Uninformative prior for alpha and beta
ab = pm.HalfFlat('ab',
shape=2,
testval=np.asarray([1., 1.]))
pm.Potential('p(a, b)', logp_ab(ab))
X = pm.Deterministic('X', tt.log(ab[0]/ab[1]))
Z = pm.Deterministic('Z', tt.log(tt.sum(ab)))
theta = pm.Beta('theta', alpha=ab[0], beta=ab[1], shape=N)
p = pm.Binomial('y', p=theta, observed=y, n=n)
trace = pm.sample(1000, tune=2000, target_accept=0.95)Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Sequential sampling (2 chains in 1 job)
NUTS: [theta, ab]
Sampling chain 0, 0 divergences: 100%|██████████| 3000/3000 [00:16<00:00, 183.25it/s]
Sampling chain 1, 0 divergences: 100%|██████████| 3000/3000 [00:13<00:00, 220.21it/s]
The number of effective samples is smaller than 25% for some parameters.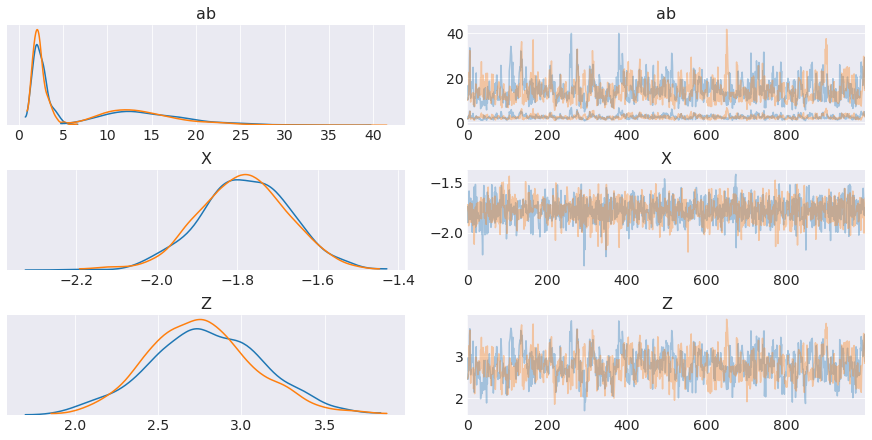
png
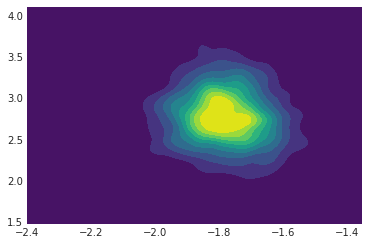
png
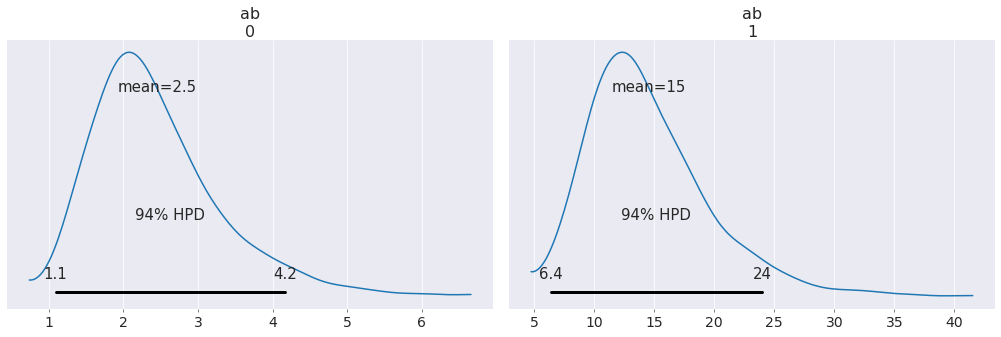
png
array([ 2.4517012 , 14.57163503])Session Info
jupyter core : 4.6.1
jupyter-notebook : 6.0.1
qtconsole : not installed
ipython : 7.10.2
ipykernel : 5.1.3
jupyter client : 5.3.3
jupyter lab : 1.2.4
nbconvert : 5.6.1
ipywidgets : not installed
nbformat : 4.4.0
traitlets : 4.3.3conda==4.8.0
conda-package-handling==1.6.0pymc3==3.8